Król i graf
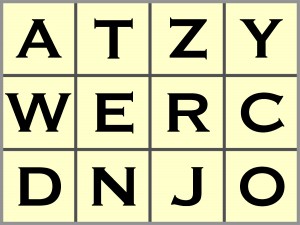
Jak wynika z Państwa komentarzy, są cztery podstawowe, różniące się nieznacznie prostokąty literowe 3×4, z których można odczytać ciąg liczebników ZEROJEDENDWATRZYCZTERY, wędrując po polach ruchem króla szachowego (pole z każdą kolejną literą sąsiaduje bokiem lub rogiem z polem z poprzednią):
oraz trzy powstające w wyniku zamiany miejscami C i Y oraz/lub D i N.
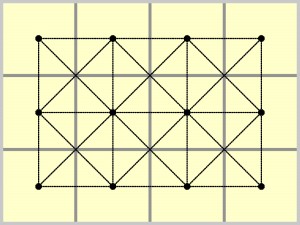
Wędrówka wiedzie fragmentami grafu zwanego królewskim, czyli sieci, którą tworzą linie (krawędzie) łączące środki sąsiednich pól (węzły):
Ze względu na powtarzające się litery trasa wędrówki jest chaotyczna – w 6 węzłach król gości przynajmniej dwukrotnie i dwukrotnie przechodzi dwiema krawędziami. Rozwiązywanie zadania, czyli konstruowanie literowego prostokąta, jest więc jakby opanowywaniem chaosu.
Gdyby król wędrował bardziej elegancko, a więc gościł dokładnie raz w każdym węźle, to trasa byłaby tzw. ścieżką hamiltonowską. Tak jest w łamigłówkach zwanych hidato, hidoku lub numbrix, o których już tu wspominałem. Rozmiar i kształt diagramów tych łamigłówek bywa różny, reguły pozostają niezmienne:
do n pól należy wpisać n różnych liczb od 1 do n tak, aby każda następna sąsiadowała z poprzednią (wprost lub na ukos).
Inaczej mówiąc, pola z kolejnymi liczbami wyznaczają ścieżkę hamiltonowską. Część liczb jest ujawniona.
Poniższe hidato do łatwych nie należy:
W rozwiązaniu wystarczy podać pięć liczb, które znajdą się w środku i w rogach diagramu.
I dodatkowa zagadka. Nawet jeśli ktoś nie upora się z tym zadaniem, to może mieć pewność, że w rozwiązaniu liczba kroków na ukos będzie parzysta. Dlaczego?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
W środku jest 32, w rogach: 40,46,16,22
22,16,32,40,46. To hidato nie jest łatwe, ale może być jeszcze trudniejsze. Można usunąć liczbę 41 i w dalszym ciągu rozwiązanie będzie jedno.
Srodek – 32
Rogi – 22, 16, 40, 46
a