Sudoku kontra spam

25 listopada 2007
Marek Penszko

W komentarzach do poprzedniego wpisu Andrzej wyraził opinię, że tzw. „nikomu niepotrzebna (nie potrzebna?) robota” jest istotą matematyki rozrywkowej. Zdarzają się jednak wyjątki potwierdzające tę regułę. Na przykład ostatnio w mediach pojawiła się informacja o projekcie wykorzystania łamigłówek matematycznych jako oręża w walce ze spamem. Autorem projektu jest Paul Gardner-Stephen z Flinders University w Adelajdzie. Nie wchodząc w szczegóły, pomysł tylko nieznacznie różni się od kilku podobnych, z których pierwszy powstał się już na początku lat 90., a potem był kilkakrotnie modyfikowany. W styczniu 2004 roku o jednym z nich wspominał Bill Gates, jako o zagadnieniu, nad którym prowadzone są prace w Microsofcie, stwierdzając przy okazji, że za dwa lata spam będzie już tylko wspomnieniem. Fachowcy bardzo szybko skorygowali tę optymistyczną zapowiedź, a rzeczywistość skłoniła ich po dwóch latach do wyrażenia opinii, iż końca zarazy niechcianej poczty nie widać. Między innymi dlatego, że zbyt silne jest środowisko, które można by nazwać spamowym lobby. Wprowadzenia na szerszą skalę pomysłu australijskiego informatyka też nie należy się spodziewać wcześniej niż za 5-10 lat, ze względu na wiążącą się z tym konieczność modyfikacji oprogramowania na serwerach.

Istota łamigłówkowych pomysłów antyspamowych oparta jest na tzw. systemie Proof-of-work, a zwłaszcza na jego dwóch najbardziej znanych wariantach – Hashcash i Penny Black. Idea jest prosta: jeśli chcesz, domniemany spamerze, abym odebrał mail, który do mnie wysłałeś – to płać, ale nie pieniędzmi, tylko roboczogodzinami twojego procesora.
Podejrzana przesyłka zostaje zatrzymana przez filtr antyspamowy, a do komputera, z którego ją wyekspediowano, wędruje łamigłówka. Odesłanie jej rozwiązania stanowi warunek odbioru poczty, zaś stopień trudności zadania zależy od tego, jak bardzo podejrzany jest oczekujący na audiencję mail. Jeśli komputer nadawcy zostanie choćby na kilka minut wplątany w łamigłówkę, to przy częstym wplątywaniu tempo rozsyłania reklamówek może zostać tak radykalnie ograniczone, że interes stanie się nieopłacalny.

Pytany o konkrety Paul Gardner-Stephen wyjaśniał, że łamigłówki powinny być takie, aby ich tworzenie, wysyłanie i sprawdzanie rozwiązania zabierało – w przeciwieństwie do rozwiązywania – jak najmniej czasu. Przyparty do muru zgodził się, że taką łamigłówką może być sudoku, bo spełnia podane warunki. W rzeczywistości jednak, gdyby ograniczyć się do klasycznych zadań, komputer spamera – wyposażony w bardzo łatwo dostępny program rozwiązujący – tylko by się uśmiał z takiej przeszkody. Należałoby więc podsyłać mu jakieś wymyślne odmiany, na przykład taką jak poniższa, zwana sudoku Y. Czym różni się ten wariant od zwykłego sudoku – oto zagadka. Łatwa dla tych, którzy znają sudoku X. A dla pozostałych i dla komputerów – trochę trudniejsza.

Suds.jpg

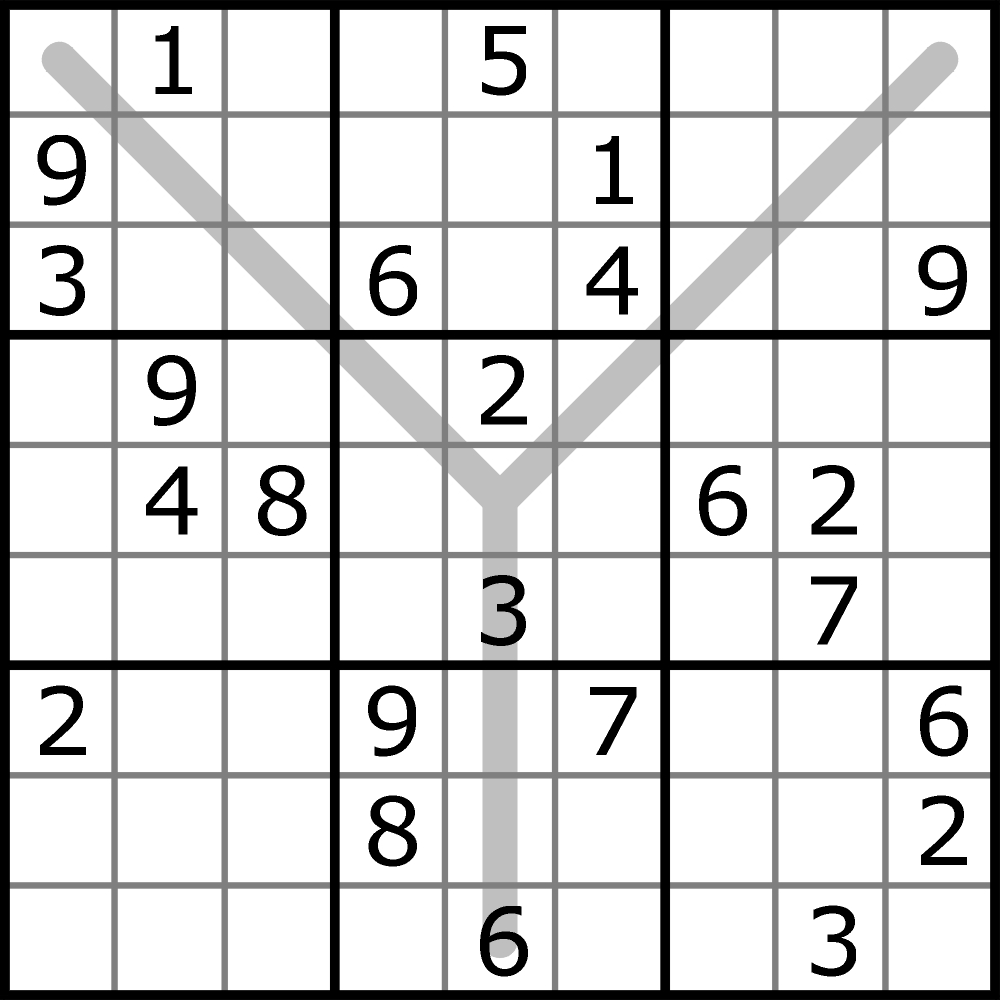
PS Komentarze z rozwiązaniem (także tylko z podaną dodatkową regułą sudoku Y) uwolnię tuż przed kolejnym wpisem za dni parę.