Alibi: bila
Mogłoby się wydawać, że określenie „matematyka bilarda” dotyczy spraw ściśle związanych z popularną grą, czyli z ruchem kul na prostokątnym stole z łuzami lub bez. W rzeczywistości to tylko mały skrawek tematu określanego jako „bilard matematyczny”, bowiem temat nie ogranicza się do prostokąta. Analizowane jest poruszanie się kul, a właściwie punktów materialnych, wewnątrz dowolnych obszarów – niekoniecznie regularnych, ograniczonych liniami prostymi i płaskich (przed laty w Łamiblogu było o grze na stole elipsoidalnym). Pozostaje, oczywiście, to, co najważniejsze, czyli zasada „kąt padania równa się kątowi odbicia”, ale pomija się resztę fizyki, która dla bilardzistów, a zwłaszcza dla snookerzystów, ma decydujące znaczenie. W bilardzie matematycznym opór nie występuje, a więc nie ma tarcia, czyli odpadają wszystkie „sztuczki” związane np. z rotacją. Uderzona w jakimś kierunku kula toczy się dotąd, dopóki matematyk jej nie zatrzyma. Stąd elementarne zadania w rodzaju:
Bilę znajdującą się przy brzegu stołu bez łuz, w połowie dłuższego boku, pchnięto pod kątem 45 stopni. W jakiej odległości od punktu startowego znajdzie się ona w momencie 59 zetknięcia się z brzegiem stołu.
Sprawa byłaby trywialna na kwadratowym stole. Wydłużając jeden bok, nieco ją komplikujemy. Gdyby ktoś miał ochotę na wyliczankę, podaję wymiary stołu – 2 na 6 metrów, czyli dalekie od bilardowych realiów.
Mniej elementarne przykłady, nie ograniczające się do prostokąta, można znaleźć np. w książkach Hugona Steinhausa (Kalejdoskop matematyczny, 100 zadań). Profesor był miłośnikiem praktycznej gry, co przełożyło się na zainteresowanie problemami teoretycznymi.
Znam tylko jeden rodzaj logicznych łamigłówek bilardowych – na prostokątnym… pokratkowanym stole. Trafiłem nań przed paru laty w pewnym japońskim piśmie. Oto przykład:
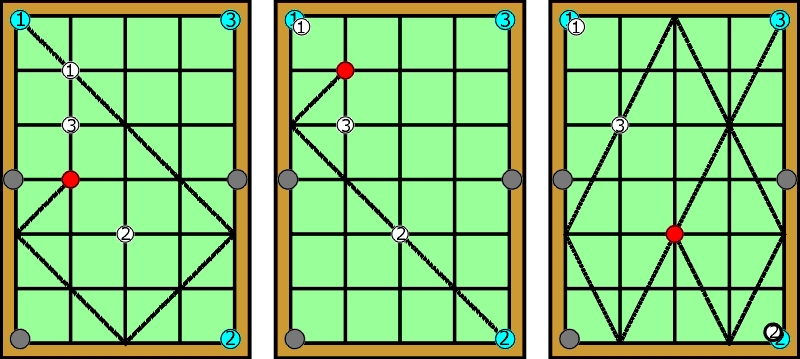
X białych bil należy x uderzeniami w czerwoną powbijać do x łuz (kolorystyka odpowiada bilardowi rosyjskiemu). Każda bila powinna wpaść do innej łuzy. „Czynnych” (niebieskich) jest zawsze tyle łuz, ile jest białych bil, czyli w przykładzie trzy. Bile mogą odbijać się od brzegu wyłącznie w punktach wyznaczonych przez linie dzielące diagram. Czerwona, uderzając w białą, zatrzymuje się na jej miejscu.
Jako rozwiązanie wystarczy podać przyporządkowanie białym bilom i łuzom liczb od 1 do x. Liczby te oznaczają kolejność: wpadających bil oraz łuz, do których są wtaczane.
Rozwiązanie przykładu: ABC = 132, abc = 132.
Poszczególne uderzenia wyglądały tak:
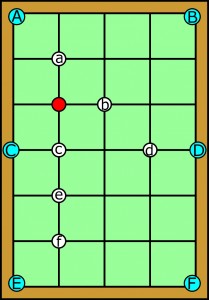
Kolej na zadanie domowe:
A na zakończenie zapraszam nie tylko dzieci na filmik sprzed ponad 50 lat (także ze względu na sentyment do starych kreskówek), w którym Donald bierze lekcję podstaw matematyki bilarda karambolu.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Kolejność wbijania bil:
e-C, b-E, a-A, c-F, d-D, f-B.
Pozdrawiam, Ola
Według innego systemu zapisu to będzie tak:
ABCDEF=361524, abcdef=324516
1) e do C
2) b do E
3) a do A
4) c do F
5) d do D
6) f do B
ABCDEF=361524
abcdef=324516
a
PS bardzo pomyslowa zabawa
Pozwolę sobie dodać, że jest jeszcze bilard zewnętrzny. Czyli na zewnątrz (sic!) obszaru.
(Każda trajektoria ma być styczna do brzegu obszaru o długości takiej by punkt styczności wypadał w połowie danego fragmentu trajektorii)
Dopiero znalazłem chwilę czasu na to zadanie i potwierdzam powyższe rozwiązania 🙂