Bez Gaussa
Gdybym miał wskazać jedną cechę różniącą matematykę rekreacyjną od „poważnej” szkolnej, byłaby to niekonwencjonalność. Na przykład, poważne rozwiązywanie układu równań liniowych wymaga skorzystania z metody Gaussa albo jakiegoś innego z kilku możliwych sposobów. Natomiast w „niepoważnych” i z reguły nieskomplikowanych okolicznościach główną rolę odgrywa pomysłowość, spryt i spostrzegawczość – choć droga do celu może być kręta i wyboista. Oto konkretny przykład z układem równań liniowych związany.
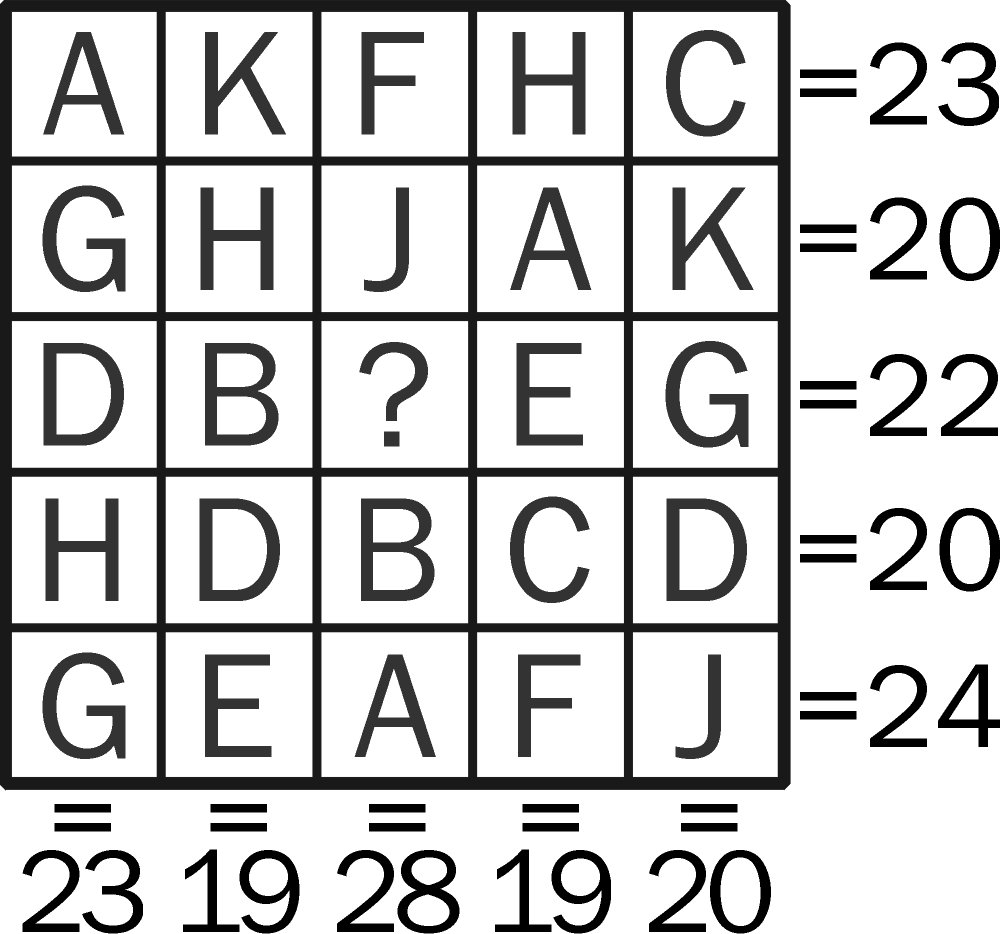
Każda z dziesięciu liter w diagramie – od A do K (pominięte jest I, żeby nie myliło się z 1) – zastępuje jedną z cyfr od 0 do 9. Obok diagramu podane są sumy pięciu cyfr w każdym rzędzie i w każdej kolumnie. Zadanie polega na przypisaniu każdej literze właściwej cyfry. A zacząć warto od odpowiedzi na pytanie o znak zapytania: jaką cyfrę zastępuje?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
A_B_C_D_E_F_G_H_J_K
7_9_3_4_1_8_6_0_2_5
[A,B,C,D,E,F,G,H,J,K] = [7, 9, 3, 4, 1, 8, 6, 0, 2, 5]
? = 2
A = 7, B = 9, C = 3, D = 4, E = 1, F = 8, G = 6, H = 0, J = 2, K = 5.
Pod znakiem zapytania mamy literę J.
?=J, A=7, B=9, C=3, D=4, E=1, F=8, G=6, H= 0, J=2, K=5.
a 7
b 9
c 3
d 4
e 1
f 8
g 6
h 0
j 2
k 5
Ale bez pomocy komputera to ciężko mi to szło.
75803
60275
49216
04934
61782
Świetne zadanie, kusi, by się pochwalić sposobem rozwiązania, zaczynając rzeczywiście od znaku zapytania: suma liczb w pierwszym i trzecim wierszu od góry razem wynosi 45, a więc tyle, ile wynosi suma liczb od 0 do 9. Tak się składa, że mamy tam 9 różnych liter, czyli znak zapytania to będzie ta brakująca, a więc J.
Następnie jest dość prosto zauważyć, że K = E+4 (pierwszy rząd – czwarta kolumna), nieco trudniej, że F = H+8 (wiersze z GAJem, czyli 2 i 5, uwzględniając K = E+4), wreszcie okazuje się, iż B = C+6 (rząd 3 – kolumna 5). I tu zaczęły się próby i błędy, są dwie możliwości dla pary H,F, niewiele też dla B, C, po podstawieniu do rzędu 4 wychodzi, że H musi być 0, bo H+B+C musi być parzyste, a więc F = 8, a wtedy B = 9, C = 3, K = 5, E = 1. Pozostałe liczby: D = 4, A = 7, G = 6, J = 2. Oczywiście tak prosto nie było jak tu opisuję, pomijam „ślepe uliczki” przy rozwiązywaniu.
?=2=J
Taki był mój koniec — ostatnie pole, które wypełniłem. Skoro skończyłem na tym, od czego warto było zacząć, moja ścieżka naznaczona trudem była niepotrzebna.