Liczby kłamią

7 września 2024
Marek Penszko

Ostatnio tkwię dość mocno w cyklach wieżowych, więc pozwolę sobie jeszcze na krótką reminiscencję dotyczącą tego tematu – przypomnienie, podsumowanie i zadanie.
Unikalny cykl wieżowy (UCW) ma miejsce, gdy na szachownicy n×n z niektórymi zablokowanymi (nieprzechodnimi) polami można wyznaczyć tylko w jeden sposób zamkniętą trasę obejścia wieżą wszystkich niezablokowanych pól (bez goszczenia dwukrotnie w tym samym polu).
Z UCW wiążą się dwa problemy matematyczne:
– jaka jest minimalna liczba blokad L(b) dla danego n z UCW?
– ile jest różnych sposobów N(L) rozmieszczenia minimalnej liczby blokad z UCW przy danym n?
Znane dotąd odpowiedzi na oba pytania znajdują się w poniższej tabeli.

O wszystkich podanych wartościach L(b) i trzech najmniejszych N(L) wiadomo od prawie półwiecza. N(L) dla n=5 i 8 znane są znacznie krócej – podali je w komentarzach Antyp i bubka111 (wspomniał też o nich uch-ty), którzy zapewne poradziliby sobie także z n=6 i 7. Oto znalezione ostatnio przez nich 12 ustawień z L(b)=3 i UCW dla n=5.

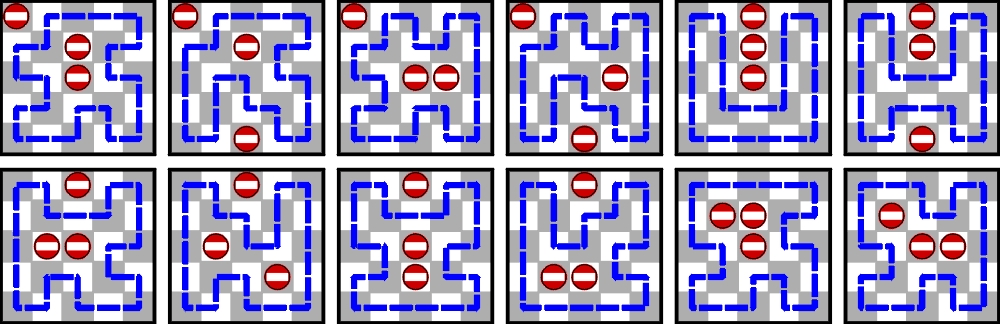
Mimo braku dowodu wiele wskazuje na to, że są to wszystkie możliwe ustawienia trzech blokad z UCW na szachownicy 5×5, choć „dowodem” może być wykorzystanie komputera. A poza tym dla n=5 sprawdzenie „na piechotę” wszystkich podejrzanych o UCW ustawień nie jest aż tak żmudne, aby było niemożliwe. Interesujący jest zaproponowany przez uch-ty w komentarzu „dwupak”, ale trudno uznać parę lustrzanych UCW za jeden cykl unikalny.

Istnieje kilkanaście rodzajów zadań diagramowych, polegających na wyznaczaniu UCW. Niemal we wszystkich liczba blokad jest większa od minimalnej, zwykle znacznie. Ponadto większość tych zadań jest jakby dwuetapowa, bowiem rozwiązywanie polega nie tylko na rysowaniu zamkniętej trasy wieży, ale także na wcześniejszym lub równoczesnym ujawnianiu niektórych lub wszystkich blokowanych pól.
Najciekawszym rodzajem tych zadań jest moim zdaniem yajirin vel yajilin – dziełko z tokijskiej „fabryczki” Nikoli, liczące sobie ćwierć wieku . Diagram zawiera tzw. liczbostrzałki umieszczone w niektórych polach. Każda wskazuje kierunek, w którym w danym rzędzie należy ulokować tyle blokad (zaczernić pola), jaka liczba towarzyszy strzałce. Poza tym:
– pola z liczbostrzałami także stanowią blokady, więc UCW powinien je omijać;
– pola z blokadami (czarne) nie mogą graniczyć bokami;
– nie wszystkie czarne blokady muszą być wskazane przez liczbostrzałki.
Poniżej znajduje się mały przykład (w rozwiązaniu jest jedna niewskazana czarna blokada) oraz większe zadanie domowe.

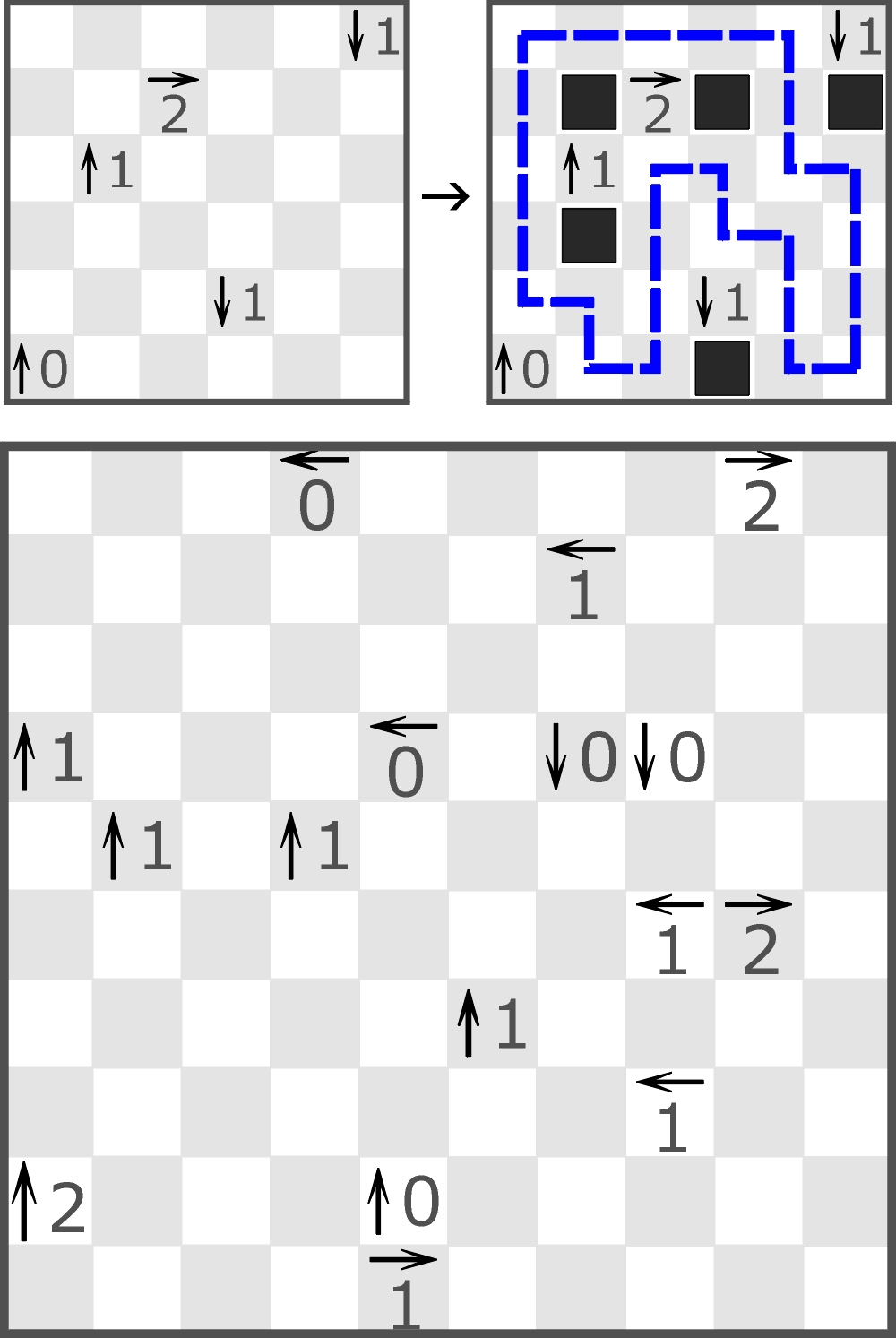
Chodzi oczywiście o zaczernienie wszystkich blokowanych pól i oznaczenie UCW, ale – uwaga! – to zadanie jest nietypowe – przewrotne i podstępne, bowiem liczby w liczbostrzałkach „kłamią”, czyli żadna z nich nie jest właściwa – nie wskazuje prawdziwej liczby blokad.
W rozwiązaniu wystarczy podać liczbę załamań wieżowej trasy. Dodam, że jest to liczba pod pewnym względem szczególna.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.