Trójkowo
Działaniem typowym dla arytmetyki szkieletowej jest mnożenie. Szkielet tworzą miejsca po cyfrach (zwykle puste kratki) w zapisie słupkowym działania, którego rekonstrukcja jest celem. Klucz do celu, czyli do rozwiązania, stanowią niektóre ujawnione cyfry (w czynnikach i/lub w iloczynach – cząstkowych i końcowym) oraz ewentualnie jakieś dodatkowe warunki. Zadanie jest tym lepsze autorsko, im bardziej wątpliwa wydaje się jednoznaczność jego rozwiązania w kontekście liczby i rozmieszczenia ujawnionych cyfr oraz liczby warunków dodatkowych (najlepiej jeśli wcale ich nie ma). No i oczywiście do rozwiązania powinna prowadzić umiarkowanie wyboista ścieżka logiczna. Oto dwa przykłady nie całkiem idealne, ale przynajmniej bez dodatkowego warunku:
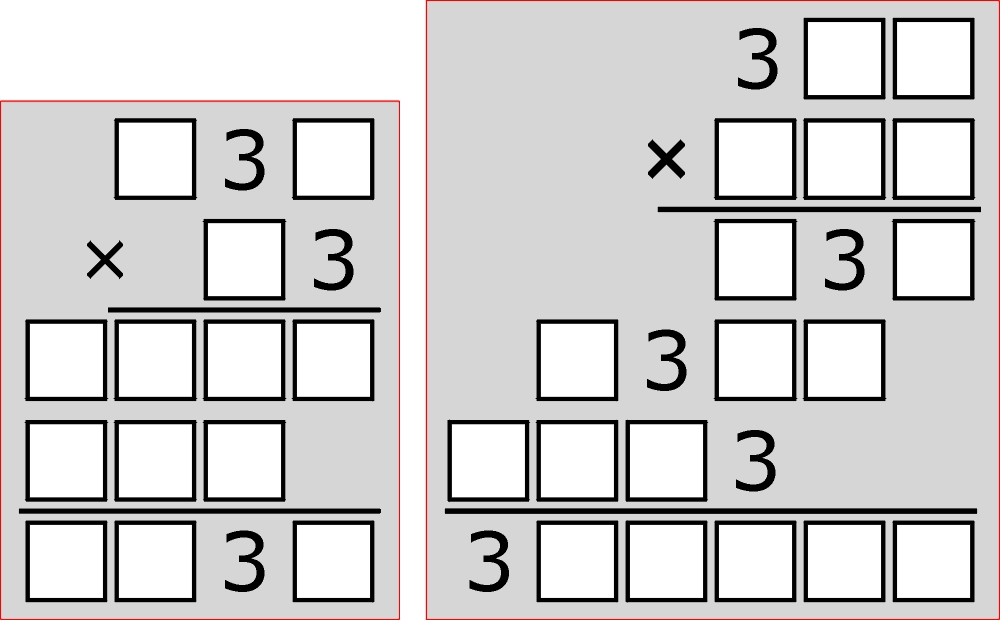
Idealnie nie jest, bo jedno z zadań ma więcej niż jedno rozwiązanie. Które i którą kratkę należałoby w nim zastąpić jeszcze jedną trójką, aby liczba rozwiązań zmalała do jednego?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Pierwsze:
432×23
Drugie:
367×992
337×971
Jak się dołoży 3 w pierwszym wierszu na drugim miejscu to zdaje się być jednoznaczne.
Oj nie.
mp
Komputer znalazł mi dokładnie po jednym rozwiązaniu dla każdego przypadku.
432*23 i 367*992
KOmputerze popraw się.
mp
432×23=9936
337×941=317117, 337×971=327227, 367x 992=364064. Trójką należy zastąpić pierwszą lub ostatnią kratkę w środkowym cząstkowym iloczynie albo drugą kratkę w trzecim cząstkowym iloczynie.
Dokładnie tak!
mp
Zadanie pierwsze
432 x 23 = 9936; 1296 864
Zadanie drugie ma trzy rozwiązania
337x 941= 317117; 337 1348 3033
337x 971= 327227; 337 2359 3033
367x 992= 364064; 734 3303 3303
Aby rozwiązanie było jedno należy inaczej ustawić trójki w liczbach pomocniczych
1.xx3
2.bez zmian
3.xx3x
Rozwiązanie
393x 961= 377673; 393 2358 3537
Stawiam na nieparzyste a zarazem na parzyste.
Znaczy się, że prawe zadanie ma nieparzystą (>1) liczbę rozwiązań, ale można to „naprawić” na parzystą liczbę sposobów.
Z rozpędu przyjąłem, że wszystkie 3 w mnożnej i mnożniku są ujawnione i wyrzuciłem je z poszukiwań 🙂