Egalitaryzm
Rodzaj krzyżówki działań zwany trzy po trzy jest typowy dla przełomu roku i pojawia się z tej okazji w Łamiblogu, gdy gospodarzowi nic oryginalnego nie wpadnie do głowy. Nieco pejoratywna nazwa wiąże się oczywiście ze splotem trzech działań poziomych z trzema pionowymi, a dodatkowo w każdym działaniu „działają” trzy cyfry.
Przypomnę, że w puste kratki należy wpisać dziewięć różnych cyfr – wszystkie oprócz zera – tak, aby równości w trzech wierszach i trzech kolumnach były poprawne. Działania w każdym rzędzie należy wykonywać kolejno, czyli bez uwzględniania pierwszeństwa mnożenia i dzielenia.
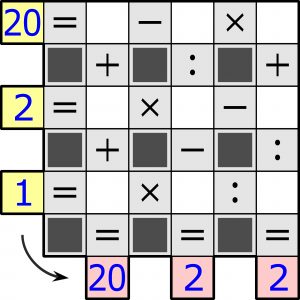
Typowość zadania uszlachetnia i… egalitaryzuje to, że żaden znak działania się nie wywyższa, czyli każdy występuje tyle samo razy.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Szczęśliwego Nowego Roku!
8 4 5
9 1 7
3 2 6
8, 4, 5
9, 1, 7
3, 2, 6
Rzędami
8-4×5
+ / +
9×1-7
+ – /
3×2/6
abc
def
ghj
=
845
917
326
8-4x5=20 + : + 9x1-7= 2 + - : 3x2:6= 1 = = = 20 2 2Rozwiązałem „w głowie”, co szczególnie satysfakcjonujące, więc podam, jak:
ABC
DEF
GHI
Jeśli A+D+G = 20, to G > 2. H nie może być 1, bo I jest różne od G, więc H musi być 2; 3 to za dużo. G*H:I to albo 4*2:8, albo 3*2:6. Skoro G<5, to zarówno A, jak i D, muszą być liczbami od 7 do 9, a więc na tyle dużymi, by musiało być E = 1. Mielibyśmy 3 możliwości dla D*1-F:
7*1-5
8*1-6
9*1-7
C musi być 4 lub 5, żeby iloczyn (A-B)*C był 20, więc F nie może być 5. F nie może być także 6, bo wtedy C musiałoby być 4 (suma C+F jest parzysta), a I – 5, tymczasem ustaliliśmy, że może być I równe tylko 6, lub 8. Stąd zostaje tylko możliwość D=9, F=7. Wtedy A=8, a G=3 i I=6. C musi być 5, a B=4 – pasuje, bo 4:1 – 2 = 2. Rozwiązanie:
845
917
326
Mądra, sprytna i pojemna główka 🙂
mp
Rozwiązanie to (idąc rzędami):
8 – 4 x 5
9 x 1 – 7
3 x 2 : 6
I wygląda na to, że jest to jedyne rozwiązanie, bo możliwe byłoby, aby w dolnym rzędzie była jeszcze trójka 4 x 2 : 8 (te rozpoczynające się od 1 i 2 odpadają), ale wtedy wynikiem dodawania w ostatniej kolumnie musi być 16, którego znowu nie da się rozbić na dodawanie 4 + inna cyfra lub 5 + inna cyfra (czego wymaga znów pierwszy rząd). Mocno lapidarne wytłumaczenie 🙂
Pozdrawiam serdecznie
Marek
845
917
326
Wszystkiego dobrego w nowym (101×10+1)×2 roku!
8, 4, 5
9, 1, 7
3, 2, 6
Przyjmując za punkt wyjścia sumę korzyści (++),
należy dywersyfikować kierunki i znaki.
Niestety, kierunek 1=3×6:2 odrzucony.
8, 4, 5
9, 1, 7
3, 2, 6