Tokio
Pięć splecionych kół olimpijskich wyznacza dziewięć ograniczonych łukami okręgów obszarów.

Obszary są lepiej widoczne, jeśli koła poddać „kwadraturze”, a obszary oznaczyć jako białe i szare.
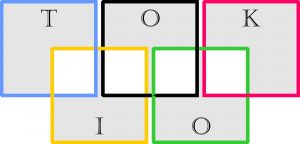
Zadanie polega na wpisaniu w te obszary dziewięciu różnych cyfr – od 1 do 9. Należy to zrobić w taki sposób, aby suma liczb w każdym kole była taka sama. Poza tym ponumerowane koła „O” (czarne i zielone) powinny mieć następującą własność: żadne dwie z trzech znajdujących się w każdym z nich liczb nie mogą być kolejnymi, czyli różniącymi się o 1.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
7 , 3 , 9
6,2,8,4
5 , 1
albo
5 , 4 , 8
9,3,7,6
2 , 1
9 6 8
2413
5 7
Ja widzę pięć splecionych kół olimpijskich… coś nowego, o czym nie wiem?
Przesadziłem. Poprawiłem. Dziękuję.
mp
Łańcuszek pól w kolejności splatania kół :
925461738
Wprawdzie intuicja podpowiadała, że 8 i 9 znajdą się w kołach skrajnych, ale to było jednak za mało.
Zadziałała metoda ścisłej eliminacji możliwości dla pola w którym znalazła się ostatecznie „1”.
Ołówek i gumkę warto zastąpić żetonikami z cyferkami 1-9, żeby palce giętkie mogły szybko zrobić to, co pomyśli głowa.
9 6 8
2 4 1 3
5 7
chyba tak
9 ,6 , 8
2,4,1,3
5 , 7
Pola „O” to 6+4+1 oraz 1+3+7
968
2413
57
Dla jednoznaczności oznaczeń przemianowałem stolice igrzysk na TOKIU.
Olimpijskie, jednoznaczne rozwiązanie występuje dla sum 11 w 5 kołach:
TT=9 OO=6 KK=8
TI=2 OI=4 OU=1 KU=3
II=5 UU=7
Faktycznie:
T=TT+TI=9+2=11
O=OO+OI+OU=6+4+1=11
K=KK+KU=8+3=11
I=II+TI+OI=5+2+4=11
U=UU+OU+KU=7+1+3=11
i w każdym kole różnice liczb > 1.
I co ja robię w tym Tokiu?
9_,_,6_,_,_8
_,_2,4,1,3_,_
_,_5,_,_,7_,_
(plus symetria)