Gruba grobla

2 lipca 2010
Marek Penszko

Dwa wpisy temu podałem reguły nurikabe. Wśród warunków, które powinno spełniać rozwiązanie, były następujące:
– Grobla stanowi jeden wielokąt, pokrętny i rozgałęziony, który  nigdzie nie obejmuje kwadratu 2×2 kratki.
To standardowa reguła, podawana zawsze, ale czy oba umieszczone w niej warunki są konieczne?
Patrząc na rozwiązanie jakiegoś nurikabe, np. poniższe zadania z przedpoprzedniego wpisu, można dojść do wniosku, że warunek dotyczący unikania na grobli kwadratu 2×2 jest zbędny.

Czarno-biały układ wydaje się optymalny, czyli zaczernienie jakiejkolwiek kratki, a więc także takie, po którym grobla pogrubieje, doprowadzi do sprzeczności z jakąś regułą (zostanie podzielony lub zmniejszony staw, trzeba będzie go powiększyć w innym miejscu, a to z kolei doprowadzi do przerwania spójności grobli). Bywa jednak tak, że można znaleźć rozwiązanie także z pogrubioną w jakimś miejscu groblą, choć w zadaniu, którego rozwiązanie znajduje się powyżej (przypominam – to nurikabe sprzed 19 lat, pierwsze opublikowane) nie jest to możliwe, czyli warunek z kwadratem 2×2 jest w tym przypadku rzeczywiście niepotrzebny.

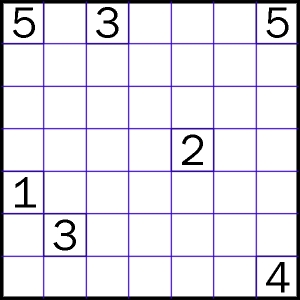
Warto jednak zwrócić uwagę, że warunek ten należy do takich, dzięki którym łamigłówka jest logiczna i przyjemna w rrozwiązywaniu, bowiem wyznacza on wyraźną ścieżkę dedukcyjną, wiodącą do celu. Aby przekonać, że jego brak „psułby” zabawę, proszę spróbować rozwiązać poniższe nurikabe, zapominając o konieczności unikania na grobli kwadratów 2×2.

Będzie trochę dłubaniny i błądzenia, a ponadto niejedno rozwiązanie (ile?). Jeżeli jednak o kwadratach 2×2 pamiętać, czyli stronić od miejscowo grubej grobli, to droga do celu okaże się bardzo łatwa i przyjemna, a cel unikatowy.

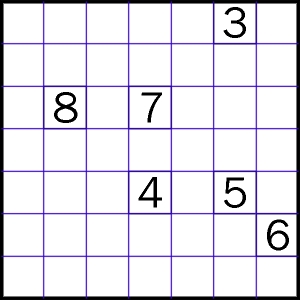
Na deser proponuję proste zadanie, którego reguły różnią się nieznacznie od nurikabe. Na czym polega różnica – to także zagadka. Zapewne nietrudna, skoro wiadomo, że w tym wpisie kręciliśmy się wokół grobli.

W każdym rozwiązaniu wystarczy podać, ile czarnych kratek, tworzących groblę, jest w sumie na przekątnych i przy brzegach diagramu.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.