Ku niewiadomej
Jeżeli pokój ma nieparzystą liczbę drzwi i przez każde wolno przejść tylko raz, to wchodząc ostatnimi, dotąd „nie zaliczonymi” drzwiami, już z pokoju nie wyjdziemy. Pokojowa wędrówka z wpisu sprzed tygodnia może się więc zacząć i skończyć w pomieszczeniach z nieparzystą liczbą drzwi, ale jeśli poza tymi dwoma skrajnymi są inne „nieparzyste” pokoje, to jedne z wiodących do każdego z nich drzwi pozostaną nietknięte. Aby zatem ustalić, czy przejście jednym ciągiem przez wszystkie drzwi jest możliwe, wystarczy policzyć, ile ich jest w każdym pokoju. Gdy „nieparzystych” pokoi jest więcej niż dwa, to przejść za jednym zamachem przez wszystkie drzwi nie sposób. Należy przy tym pamiętać, że obszar poza M-ileś także traktujemy jak pokój, więc istotna jest również suma drzwi w ścianach zewnętrznych.
Powyższe proste „reguły gry”, ktore podal w komentarzu także Andrzej69, znane są od prawie dwóch wieków. Natomiast przed półwieczem na łamach Scientific American Martin Gardner zauważył jako pierwszy, że zadanie z lokalem M-5 można rozwiązać, przenosząc się z płaszczyzny na torus. Jeśli na takiej powierzchni, przypominającej kształtem obwarzanek lub detkę, narysujemy układ pięciu pokoi z wpisu „M-5 i więcej” tak, że otwór „otoczony” przez torus, znajdzie się w jakimś nieparzystym pokoju, to pokonanie wszystkich drzwi będzie możliwe. Sekret polega na tym, że tak narysowany na powierzchni torusa pokój-prostokąt w gruncie rzeczy nie ma wnętrza – punkty po przeciwnych stronach jego brzegu da się połączyć linią nie przecinającą tego brzegu, czyli z pokoju można się wydostać nie korzystając z drzwi.
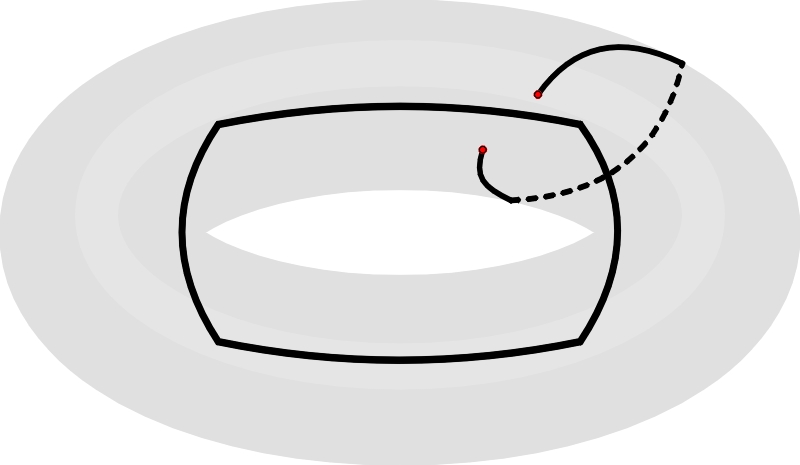
Choć toroidalnie sytuacja wygląda elegancko, to w istocie sprowadza się do topologicznie równoważnego chwytu poniżej pasa – narysowania M-5 na płaskiej prostopadłościennej płytce i zrobienia otworu na wylot w pokoju z nieparzystą liczbą drzwi. W trakcie wędrówki wydostajemy się przez ten otwór na spód płytki i ścianką boczną docieramy na wierzch. Inaczej mówiąc, wykonujemy podkop, czyli jakby dodatkowe drzwi.
Z zadań pokojowych chciałbym przypomnieć jeszcze jedno – labirynt dla zbieraczy, w tym przypadku liter.
Zaczynamy od pokoju z P, biorąc zeń znajdującą się w nim literę i – w drogę. Celem jest dotarcie do niewiadomej, czyli do pomieszczenia z X. Wchodząc po drodze do jakiegoś pokoju, trzeba wziąć znajdującą się w nim literę i nie wolno się jej pozbywać. Pokoje bez litery stają się niedostępne. Drzwi do X otworzą się tylko wtedy, gdy będziemy mieć ze sobą 24 różne litery, każdej tylko po jednej sztuce. Wąskiej drogi przez 23 pokoje!

Komentarze
Pokojowa ścieżka:
P,O,I,G,H,M,S,U,W,J,Z,R,L,C,Ł,Y,T,E,D,A,N,F,K,B,X.
Witam.
Rozwiązanie „Labiryntu dla zbieraczy”:
POIGHMSUWJZRLCłYTEDANFKBX
Pozdrawiam
Piotr
Wąska dróżka przez labirynt wygląda tak:
P-O-I-G-H-M-S-U-W-J-Z-R-L-C-Ł-Y-T-E-D-A-N-F-K-B-X.
Dziękuję za przyjemną choć niełatwą wędrówkę.
Enzo
Rozwiązanie „pokojowych literek”:
POIGHMSUWJZRLCŁYTEDANFKBX
Ciekawostką jest to, że ta łamigłówka, pozornie wymagająca podejścia intuicyjnego i na „chybił trafił”, okazuje się być bardzo logiczna. Aby ją rozwiązać nie trzeba robić żadnych założeń, ale, jak najbardziej metodą dedukcji – krok po kroku, eliminować pola, które należy ominąć, a wyłapywać te, przez które powinno się przejść. Wtedy wszystko okazuje się jednoznaczne i spójne, a rozwiązanie „samo” 😉 wychodzi.
Pozdrawiam
AB
Panie Marku,
Mam pytanie (nie będę ukrywać – wyłącznie z czystej ciekawości):
Czy ten wpis nie został przez Pana utworzony bezpośrednio po wcześniejszym wpisie „pokojowym” – „M-5 i więcej” (a może i równocześnie z nim), a przed obydwoma walentynkowymi?
Naturalnie przed upublicznieniem musiałby być przynajmniej nieznacznie zmodyfikowany (choćby ze względu na odniesienie do komentarzy), ale nie chodzi mi o czas jego finalizacji, tylko o moment rozpoczęcia i ewentualnie powstania jego „lwiej części”.
Jeśli przypadkiem mam rację, to zagadka (choć chyba niezbyt trudna i zdecydowanie nie na logikę, a raczej na spostrzegawczość): skąd to wiem? 😉
Pozdrawiam
AB
Panie Andrzeju69, ma Pan rację – ten wpis powstał przed Walentynkami, które się potem „wcięły” w blog.
Spróbuję rozwiązać zagadkę, choć nie wiem, czy starczy mi cierpliwości i spostrzegawczości. Jeżeli w ciągu 3 dni nie podam rozwiązania, to znaczy, że się poddaję i proszę o odpowiedź.
A poza tym zagadka, jak sądzę, jest dla wszystkich, więc przegram także, gdy rozwiązanie poda wcześniej w komentarzu ktoś inny.
Pozdrawiam
mp
Dziękuję Panie Marku za odpowiedź i czekam na rozwiązanie.
Pozdrawiam
AB
PS: Zagadka oczywiście jak najbardziej dla wszystkich.
Ponieważ wpis przedwalentynkowy kończy się „… o tym następnym razem”, a wpis po walentynkowy zaczyna się „Jeżeli…” i dalej jest wyjaśnienie, stąd wniosek, że Pan Marek pisał te dwa wpisy równolegle. Mało tego, można sądzić, że wiele wpisów jest już napisanych lub chociaż w zamyśle, lub pisanych jest kilka (no może bez przesady – 2, 3 wpisy naraz) w jednym czasie lub dawno przed publikacją i tylko czekają na odpowiedni moment. Co zresztą jest zupełnie zrozumiałe.
Org, gratuluję spostrzegawczości z obu powodów – rozwiązania zagadki (przypuszczam, że Andrzej69 potwierdzi poprawność) oraz słusznej uwagi dotyczącej przygotowywania wpisów, choćby w zamyśle, z niewielkim wyprzedzeniem.
Taki zapobiegliwy jestem jednak od ca 2 miesięcy (mimo to pojawiają się wpisy powstające ad hoc, jak np. walentynkowe). Przedtem z reguły po jednym wpisie pojęcia nie miałem co będzie w następnym. Było to jednak lekko stresujące, bo staram się zachować mniej więcej stałą częstotliwość, więc trochę zmieniłem strategię:)
Pozdrufka
mp
Do Orga, Pana Marka i nie tylko:
Org, wszystko co napisałeś jest jak najbardziej słuszne, ale mimo to nie stanowi odpowiedzi na moją zagadkę. Dla mnie był to co najwyżej argument dodatkowy, potwierdzający pewne spostrzeżenie, choć być może dla Ciebie będzie bardziej przekonywujący od tego, co akurat ja uważam za istotniejsze (sprawa może okazać się subiektywna – ocenisz to sam).
Moim zdaniem zakończenie wpisu „…o tym następnym razem.” świadczy niewątpliwie o zamiarach (czyli jak sam to określiłeś „byciu w zamyśle”), ale niekoniecznie musi oznaczać napisanie dalszego tekstu. Rozpoczęcie drugiego wpisu od „Jeżeli…” też nie jest według mnie zbyt mocnym argumentem. Uważam, że opieranie się tylko na tym jest dość ryzykowne. Poza tym mogłoby to też świadczyć o sporządzeniu np. tylko pewnych odręcznych notatek (które przepisane zostały jednak dopiero później), natomiast według mnie istnieje przesłanka pozwalająca domniemywać, że tekst powstał wcześniej w sensie fizycznym, tzn. był całkiem lub prawie gotowy do ukazania się w internecie, a po wpisach walentynkowych został jedynie skorygowany (choć nie wykluczam, że mogły to być nawet dość duże zmiany lub też dopisanie albo usunięcie całkiem sporego fragmentu).
Także, jak już wcześniej powiedziałem, generalnie się z Tobą zgadzam, ale nie uważam jednak tego za argument koronny.
Zagadka zatem dalej czeka na rozwiązanie, choć być może dla niektórych okaże się ono trochę nietypowe i niezbyt satysfakcjonujące.
Pozdrawiam
AB
Powiem tak, rzeczywiście jedynie zamysł potrafiłbym udowodnić, ale na pewno nie fizyczne równoległe powstawanie dwóch tekstów. Byłbym z lekka rozczarowany gdyby moja odpowiedź była tą poprawną, ponieważ równie dobrze można powiedzieć, że wspólny temat łamigłówek pozwala sądzić, że materiały były pisane jednocześnie. Czekam na rozwiązanie zagadki.
Do P. Marka, znów z innej beczki, ja jestem zwolennikiem pisania według „nowej” ortografii tzn. „niezaliczonymi”
Orgu, bo Pan jest nowy, a ja jestem stary i jak tylko wyczuwam, że imiesłów przymiotnikowy pełni funkcję czasownikową, to zaraz bym rozdzielał.
Dziękuję za uwagę, postaram się ją zapamiętać i już nie będę niepoprawny, a więc będę niepoprawiany.
Pozdrav
Pozdrav?
Czyli możemy się jutro spotkać w Żilinie?
Pozdrav
Org:
Planowałem, ale niestety mam gościa (i mam nadzieję, że gość tego nie czyta), któremu łamigłówki, a zwłaszcza sudoku, ani w głowie.
Życzę sukcesów, jeśli się Pan wybiera i proszę o garść wrażeń – także w imieniu innych łamigłówkowiczów.
Saluti cordiali (do Włoch też nie jadę, ale język nie jest mi całkiem obcy).
mp
Ponieważ rozwiązanie zagadki kolejności wpisów dotąd nie padło podam małą podpowiedź. Będzie ona typu nie wprost, czyli gdzie szukać nie należy:
Otóż, co może wydać się dziwne, odpowiedzi nie ma w tekstach wpisów! Nie ma jej w napisach „pomocniczo-organizacyjnych” (nie wiem jak je trafnie nazwać) typu: „Zapisano w kategorii…” lub „Ten wpis został opublikowany dnia…”. Nie ma jej również w komentarzach (tekstach, datach, czy nickach autorów).
Aczkolwiek nie będę ukrywać, że to właśnie komentarze mogą okazać się w jakiś sposób pomocne w odnalezieniu rozwiązania. Ale ostrzegam, że pomoc ta jest zdecydowanie nietypowa i może lepiej się tym nadmiernie nie sugerować.
Dodam też, że choć może nie zawsze, ale przynajmniej w niektórych sytuacjach (i to jak najbardziej typowych), informacje potrzebne do rozwiązania są raczej dobrze widoczne (niewykluczone natomiast, iż tam gdzie się znajdują można w ogóle nie spojrzeć).
Pozdrawiam
AB
Zagadka Andrzeja69 robi się coraz bardziej intrygująca i, jak dla mnie, coraz trudniejsza mimo, a może właśnie z powodu „podpowiedzi”.
Miałem nadzieję, że ktoś mnie wyręczy w podaniu odpowiedzi na zagadkę kolejności wpisów, ale wygląda na to, że muszę zrobić to sam.
Pisząc podpowiedź wymieniłem miejsca, gdzie rozwiązania szukać nie należy. Można to nawet bardziej rozszerzyć: nie ma go gdziekolwiek na stronie WWW!
A co w takim razie mają z tym wspólnego komentarze?
Generalnie to, że potrzebne informacje widoczne są wtedy, gdy oglądamy podstronę z pojedynczym wpisem i następującymi po nim komentarzami, a nie główną stronę blogu (gwoli ścisłości: na głównej stronie też można zaobserwować co potrzebne, ale wydaje mi się, że trudniej, bo nie jest stale widoczne).
Gdzie wobec tego te informacje się znajdują?
Jak napisałem, są dobrze widoczne, ale w miejscu, gdzie raczej rzadko się zagląda: w pasku adresowym. Jego zawartość w przypadku np. tego wpisu wygląda tak:
„http://penszko.blog.polityka.pl/?p=173”
Liczba 173 jest (pozwolę sobie na niezbyt ścisłe określenie) numerem kolejnym wpisu. Dodam, że nie bazuję tutaj na żadnej wiedzy informatycznej, a jedynie na spostrzeżeniu, jak zmienia się z odcinka na odcinek.
Tym razem było tak, że po wpisie nr 172 („M-5 i więcej”) pojawił się nr 174. Początkowo nie przywiązywałem do tego żadnej wagi i uznałem za zwykłą pomyłkę Autora lub programu. Kolejny wpis miał prawidłowo nr 175, ale następny po nim, drugi „pokojowy” („Ku niewiadomej”), nr 173!
Moją pierwszą reakcją było to, że Pan Marek „załatał dziurę”. Ale właściwie to po co? Sprawdziłem: „dziury” zdarzały się już wcześniej (choć niezbyt często), i jak dotąd chyba w niczym to nie przeszkadzało.
I dopiero za chwilę refleksja: Ten wpis po prostu musiał powstać wcześniej! Niewykluczone, że razem z pierwszym „pokojowym” jako jego kontynuacja. Prawdopodobnie został przygotowany do ukazania się, podłączony do programu zarządzającego blogiem (szczerze mówiąc nie mam pojęcia jak to działa, ale tak podejrzewam) i ukryty czekał na swoją kolej. Nie kolidowało to oczywiście z wprowadzaniem ewentualnych poprawek czy uaktualnień przed jego wyświetleniem.
Dodatkowym uzasadnieniem takiego obrotu rzeczy były użyte sformułowania (o czym wspominał Org) oraz fakt, że istniał konkretny motyw, aby gotowy już wpis przesunąć na później: oba walentynkowe teksty były związane z konkretną okazją. Nie jest to może samo w sobie żadnym argumentem, ale w tym kontekście w jakiś sposób potwierdza hipotezę. Należałoby jeszcze dodać, że nie było żadnego powodu, by działać w ten sposób z premedytacją.
Napisałem to trochę tak, jakbym sam w tym uczestniczył, ale to oczywiście tylko obserwacje i przypuszczenia. Wydaje mi się jednak, że uzasadnione. Jeśli coś wyglądało inaczej, to proszę Panie Marku mnie skorygować. Mam również nadzieję, że w niczym nie uraziłem.
Liczę się z tym, że to rozwiązanie nie dla wszystkich musi być satysfakcjonujące, ale takie właśnie ono jest.
Pozdrawiam
AB
Panie Andrzeju69, czytając Pańskie rozwiązanie zagadki czułem się jak dr Watson słuchający wyjaśnień Sherlocka Holmesa.
Jeśli miałbym coś korygować, to tylko swoją pamięć, bo to, co zdążyłem zapomnieć, powróciło dzięki Pańskiej dedukcji.
Lep pozdrav (po jakiemu to?)
mp
Lep pozdrav?
Na pierwszy rzut oka (a może lepiej ucha 😉 ) wyglądało mi to na język któregoś z krajów byłej Jugosławii. Jednak bez żadnej pomocy nie podejmowałbym się bardziej precyzyjnego określania, bo osobiście nie za bardzo rozróżniam te języki. Zresztą samo „pozdrav” jest używane chyba w kilku z tych krajów.
Po krótkim szukaniu w internecie okazało się, że to po słoweńsku.
Pozdrawiam
AB
PS: Dziękuję Panie Marku za miłe słowa.
do Andrzeja69 – jakie to proste 🙂
do P. Marka – po słoweńsku,
Pozwolę sobie zażartować, czy te pozdrowienia ma Pan z nagrań papieża :/ ?
P.S.
Refleksje ze Słowacji napiszę przy jakimś kolejnym wpisie dotyczącym sudoku.
Pozwolę sobie napisać trochę serio.
Lubię urozmaicać zakończenia maili zastępując polskie „pozdrawiam” obcojęzycznymi odpowiednikami, zwłaszcza w językach, które z jakichś powodów są mi bliskie. Taki kaprys.
Ostatni wariant wiąże się z moim starszym synem, który skończył słowenistykę.
Salutări
mp
PS W takim razie o sudoku będzie „następną razą”, zwłaszcza że nadarza się okazja, bo otrzymałem od Janosława fajną odmianę sudoku jego pomysłu.
Czytając komentarz Andrzeja69 omawiający zagadkę, miałem wrażenie, że oglądam następny odcinek serialu „CSI: Kryminalne zagadki Miami”.
„Lep pozdrav (po jakiemu to?)” – pierwsze moje skojarzenie związane było z krajem, gdzie od Szczawnicy jest na rzut beretem, czyli Słowacją. Coś mi jednak to wyrażenie pachniało po bałkańsku więc postanowiłem to sprawdzić w internecie i okazało się, że chodzi o język kraju, gdzie ciężko byłoby dorzucić beretem, czyli Słowenię.
Pozdrawiam
Ja wiem żę się wcinam , ale czy mógłby mi pan podać rozwiązanie M5 cyframi bo już nie rozumiem tego wpisu ” ku niewiadomej”
Radku 94, we wpisie „M-5 i więcej” na schemacie lokalu M-5 (dolna prawa część górnego rysunku) drzwi nie są ponumerowane, więc podanie rozwiązania liczbami byłoby kłopotliwe i chyba trochę bez sensu, bo nie chodzi o konkretne rozwiązanie (jest ich wiele) tylko o zasadę.
Może tak:
We wpisie „Ku niewiadomej” narysowany jest jeden pokój na powierzchni przypominającej kształtem dętkę koła samochodowego. Potraktuj ten pokój jako górny środkowy pokój ze schematu we wpisie „M-5 i więcej” i dorysuj do niego na dętce pozostałe 4 pokoje oraz oznacz wszystkie drzwi. Inaczej mówiąc, przenieś na dętkę schemat z wpisu „M-5 i więcej”.
Jeśli teraz będziesz rysował trasę wędrówki na dętce, zaczynając od dowolnego pokoju z nieparzystą liczbą drzwi, to z pewnością uda Ci się przejść przez wszystkie drzwi, przez każde dokładnie raz. Dlaczego? To jest wyjaśnione we wpisie „Ku niewiadomej”. Krotko mówiąc: dętka stanowi jakby dodatkowe drzwi.
Pozdrawiam
mp
Dziękuje
Ja wiem że mi pan to dokładnie wytłumaczył ale ja jestem uczniem klasy i gimnazjum no i chcę oddać pracę na matematykę miałem już jedno, drugie rozwiązanie ale mi nie wychodziło więc prosił bym pana aby jak można mógł podać mi rozwiązanie tego i jeżeli można to pan wysłał by mi rysunek na maila radek_iwan@o2.pl i bardzo prosze
Witam,
Czy mogłabym również prosić o podanie rozwiązania? Spędziłam nad tym bardzo dużo czasu, aż trafiłam na Pana stronę, jednak kompletnie nie rozumiem jak mam to zrobić… Byłabym bardzo wdzięczna za rozwiązanie. Może wreszcie usnę spokojnie..
Serdecznie pozdrawiam
AN
Ja również prosiłbym o rozwiązanie, zupełnie nie mogę się połapać a od rysowanie palce mnie już bolą. Będę wdzięczny za gotowe rozwiązanie:D
Maksie, ale o co konkretnie chodzi?
Prosiłbym też wcześniej o poczytanie komentarzy. Ich lektura może wiele wyjaśnić.
mp
A więc tak, czy da się to w ogóle rozwiązać. Sam pan pisze najpierw, że się da a na samym końcu, że da w szczególnych okolicznościach. Z komentarzy rozumiem 3 przez dziesiąte. Tępy nie jestem, ale naprawdę nie jestem w stanie tego zrozumieć. Dlatego prosiłbym o gotowe rozwiązanie M5, jeśli jest one w ogóle możliwe.
Maksie,
we wpisie „M-5 i więcej” jest rysunek domu bez dachu, a obok jego plan.
Wyobraź sobie, że dom stoi na wielkiej krze (to zielonkawe) i pływa z nią po Morzu Arktycznym.
Ponumeruj na planie drzwi – rzędami od lewej, od góry do dołu, czyli będzie tak (z grubsza):
1……..2……..3
4……5……….6……7
….8…..9….10…11
12………13……….14
……15………16
Znajdujesz się w lewym dolnym pokoju (nad drzwiami 15) i masz przejść przez wszystkie drzwi, przez każde tylko raz.
Sprawdź, czy wziąłeś ze sobą łom – to ważne.
Zaczynasz. Przekraczasz drzwi nr 9, bierzesz łom i wykuwasz najpierw dziurę w podłodze, a potem przerębel w krze. Wchodzisz do przerębla, przepływasz pod krą i wydostajesz się na jej powierzchnię naprzeciw drzwi 2. I kontynuujesz wędrówkę: 2-5-1-4-8-12-15-13-16-14-11-7-3-6-10. Gotowe!
Pozdrawiam
mp
PS Kra (plus podłoga) to torus, tylko taki trochę kanciasty.
jak to panie Marku gotowe a 9 co z nią ana musi zostać?
Nie rozumiem pytania.
Chodziło o przejście przez wszystkie drzwi i się przeszło – więc „gotowe”.
mp
PS drzwi 9 są przekraczane na początku drogi (przed zrobieniem przerębla).