Nie tylko płytki
Przed miesiącem z premedytacją zamieściłem tu zadanie nie mające rozwiązania.
Z płytek 1×2 ułożony był kwadrat 6×6.
Płytki należało poprzekładać tak, aby ich brzegi nie tworzyły wewnątrz kwadratu prostego odcinka łączącego boki, jak na przykład czerwony na rysunku. Rozwiązaniem było więc ustalenie, że nie ma rozwiązania. Kilka osób podało usprawiedliwienia, czyli dowody tej nieobecności.
Przyznam się, że początkowo podstępu nie planowałem, czyli przekładanka miała być typowa, z figurą o innych wymiarach. Nie poradziłem sobie jednak wówczas z ułożeniem takiego zadania, które nie byłoby bardzo proste lub wręcz trywialne. Czy mi się to teraz udało, pozostawiam Państwa ocenie.
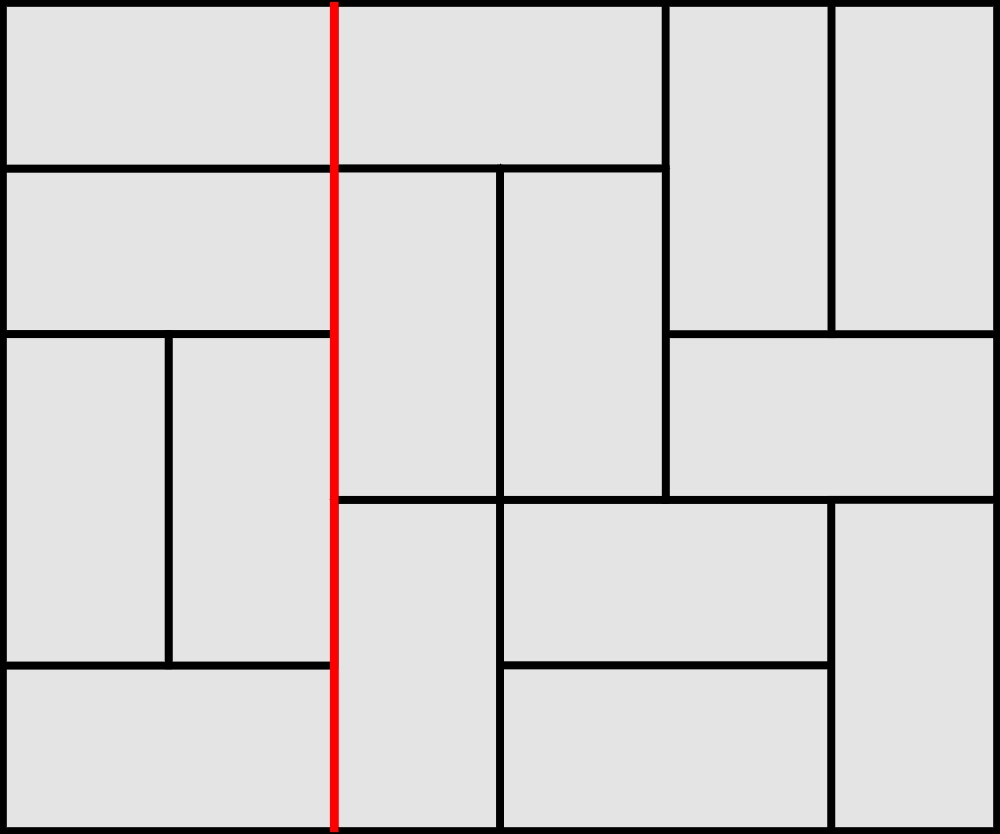
Ile co najmniej płytek trzeba przełożyć, aby zlikwidować linię prostą biegnącą krawędziami kilku płytek od boku do boku prostokąta (oznaczona kolorem), nie tworząc przy tym innej takiej linii, czyli dzielącej prostokąt 5×6 na dwa mniejsze.
Powróćmy teraz do parkieciarzy sprzed miesiąca, którzy tym razem mają do wykonania nieco inne zadanie.

Powinni wyłożyć pomieszczenie 5×8 płytkami 1×1 i 1×2. Szef zadysponował, by użyć jak najwięcej płytek 1×1, ale by płytki te nigdzie nie stykały się bokami.
Jaką maksymalną liczbę płytek 1×1 mogą wykorzystać rzemieślnicy i jakie może być ich (tzn. płytek, a nie rzemieślników) przykładowe rozmieszczenie?
A na deser urodzinowy drobiazg, bo Łamiblogowi niedawno stuknął roczek.
![]()
Objaśnienie jest, jak sądzę, zbędne, a zalecany sposób rozwiązywania – „na piechotę”, żeby główka pracowała. Nie wiadomo tylko, czy całemu organizmowi starczy wytrwałości i cierpliwości. Ile jest rozwiązań – to także zagadka (nie znam rozwiązania).

Komentarze
Tu są wszystkie rozwiązania
120061*668=80200748
120066*618=74200788
220065*319=70200735
520061*773=40200715
520062*773=40200792
620068*987=61200711
920062*763=70200730
A tu dodatkowe
120069*683=82007127
220066*912=20070019
220067*912=20070110
220068*912=20070201
220069*912=20070292
420060*478=20078868
420061*478=20078915
420062*478=20078963
420063*329=13820072
420063*478=20079011
420064*478=20079059
420065*478=20079107
420066*478=20079154
420067*478=20079202
420068*478=20079250
420069*478=20079298
520060*386=20074316
520061*386=20074354
520062*386=20074393
520062*658=34220079
520063*386=20074431
520064*386=20074470
520065*386=20074509
520066*386=20074547
520067*386=20074586
520067*608=31620073
520068*386=20074624
520069*386=20074663
620061*668=41420074
620066*618=38320078
A tego typu
120063*9012=1082007756
120063*1833=220075479
120063*2889=346862007
120063*7631=916200753
jest 511 układów.
Zadanie rozwiązałem przy pomocy prostego programu, a nie zgodnie z delikatną sugestią przy pomocy logicznego rozumowania.
Skoro mamy młodego Jubilata, to chciałbym mu złożyć najlepsze życzenia urodzinowe, ale przede wszystkim to jego niestrudzonemu Ojcu. Dalej tak trzymać Panie Marku!
Pozdrawiam
AB
120066*618=74200788
Pozdrawiam 🙂
Przyłączam się do życzeń i mam do rozwiązania dwa drobiazgi:
STO*LAT = Ł*A*M*I*BLOG
STO*LAT = ŁA+MI*BLOG
Są to dwa niezależne zadania. Nie zalecam sposobu „na piechotę” 🙂
pozdrawiam,
slawek
Witam
1.Przekładanie płytek.
Stajemy w lewym dolnym rogu parkietu.
Wytyczamy prostokąt (4 jednostki w górę, 3 jednostki w prawo) i obracamy prostokąt na drugą stronę. Położenie zmieniło 5 (pięć) płytek.
2. Starzy znajomi.
Rzemieślnicy mogą wykorzystać 12 płytek 1×1
Przykładowe rozwiązanie:
22122122
12212212
21222122
22212221
12122122
3. Deser urodzinowy
120061 x 668 = 80200748
120066 x 618 = 74200788
220065 x 319 = 70200735
Pozdrawiam
PS
Nie wiem czy powyższe rozwiązania są rozwiązaniami optymalnymi, ale wiem, że Pan Marek w ciągu minionego roku zrobił kawał dobrej roboty.
Pierwsze zadanie :
Dzięki cennemu spostrzeżeniu Andrzeja69 z parkietowego dowodu sprzed miesiąca łatwo zauważyć , że do zablokowania wszystkich siecznych potrzeba minimum 15 klepek – i dokładnie tyle występuje na parkiecie . Czyli nieparzyste sieczne pionowe są blokowane przez dokładnie jedną klepkę , a parzyste sieczne pionowe i sieczne poziome przez dokładnie dwie klepki . Po obejrzeniu sytuacji początkowej (parkiet przed poprawką) widać , że pierwsza sieczna pionowa jest zablokowana przez aż trzy klepki . I to jest ten układ , który trzeba rozbić :))
Proponuję przełożyć 5 klepek , ale bez pewności , że jest to najlepsze rozwiązanie . Patrząc na lewy dolny róg .
AAB CAA
CDB CDB
CDE –> GDB
GGE GEE
Drugie zadanie :
Łatwo wydedukować , że w parkiecie 5×8 , czyli o parzystej liczbie pól , musi być parzysta liczba klepek 1×1 . Rozwiązania z 12 klepkami łatwo sobie rozrysować . Ale udowodnić , że nie ma lepszego rozwiązania , albo pokazać rozwiązanie z 14 klepkami – to problem nad którym muszę jeszcze popracować .
Trzecie zadanie :
120061 x 668 = 80200748
120066 x 618 = 74200788
220065 x 319 = 70200735
ale tak na piechotę to troszkę można się zmęczyć .
I oczywiście najlepsze życzenia dla bloga Łami na ręce Jego pracowitego i kreatywnego Ojca. Niech nam rośnie , pięknieje i się rozwija . Łamiblog .
Pozdrowienia
AC
Witam.
Panie Marku, trochę spóźnione, ale serdeczne życzenia oraz podziękowania za rok fajnej zabawy (oby jak najdłużej trwała).
Do Antypa: podałeś 7 rozwiązań trzeciego zadania, ale tylko 3 pierwsze są poprawne (te same podał Alek) – pozostałe 4 są błędne (sprawdź sam – chyba program „obciął” Ci ostatnie cyfry w wynikach).
Do Alka: w drugim zadaniu chyba nie ma możliwości ułożenia 14 klepek 1×1 (12 to max).
Pozdrawiam
Piotr
A czy nie wystarczy w zad. 1 przełożyć 4 płytki?
Patrząc od dołu lewego rogu przełożyć 3 płytki z lewej str. czerwonej linii i 1 płytkę z dołu z prawej str. Trzy z nich „stały”, jedna „leżała”. Po zmianie 3 będą „leżały”, jedna „stała”. „Stać” będzie tylko ta w dolnym lewym rogu?
Do Jawa :
niepoprawnie – otwiera się sieczna pozioma , druga od dołu .
A moje rozwiązanie z 5 klepkami trochę się przesunęło .
Powinno być :
AAB–>CAA
CDB–>CDB
CDE–>GDB
GGE–>GEE
Klepka DD jest nieruchoma , a klepki AA , BB , CC , EE i GG „obracają się” dookoła niej.
Do Piotra44 :
Masz rację – 12 płytek 1×1 to max , tylko jak to udowodnić ?
Pozdrowienia
AC
Do jawy: pojawi się wtedy pozioma linia dzieląca prostokąt 5×6 na dwa mniejsze.
Pozdrawiam
Piotr
@jawa: nie, jesli dobrze zrozumiałem Twoj pomysł z przłożeniem tylko 4 płytek, to w ten sposób który podałeś powstanie pozioma linia przez całą planszę.
Ja również niczego lepszego niż przełożenie 5 płytek (tych samych co pisali koledzy wyżej) nie potrafiłem wymyślić.
A co do drugiego zadania, to więcej niż 14 sie chyba nie da, bo probowalem na rózne sposoby i zawsze 12 mi wychodzi.
pozdrawiam
(poprzedni koment chyba wcielo)
@jawa, jesli dobrze zrozumialem co miales na mysli z tymi 4 plytkami, to Twoj sposob jest bledny bo powstanie pozioma linia przez caly parkiet.
raczej to 5 plytek (wspominali o tym koledzy wyzej) jest najbardziej optymalne.
co do drugiego zadania, to mnie rowniez nie udalo sie uzyskac 14 plytek. zawsze 12 wychodzi.
Ale Pan podkręcił tempo Panie Marku!
Nawet nie zdążyłem wysłać rozwiązań. W szczególności, że „urodzinowy torcik” okazał się w moim przypadku dość ciężkostrawny 😉 . Muszę przyznać, że jego rozwiązanie zalecaną metodą „na piechotę” zajęło mi dość dużo czasu, gdyż zagadka, choć w sumie nietrudna, była wyjątkowo pracochłonna.
I tu pytanie do Pana jako autora, jak również do innych „główkołamaczy”: Czy istnieje na to jakaś sprytna, chociaż może trudna do odkrycia, metoda, dzięki której rozwiązanie przychodzi szybko? Czy też pozostaje tylko wyjątkowo żmudna analiza „kawałek po kawałku”, jak to było w moim przypadku?
Dodam jeszcze, że gdy w końcu uporałem się z tym zadaniem, to spróbowałem jeszcze metodą dla leniwych. Napisanie miniprogramiku (składającego się w praktyce tylko z jednej, choć rozbudowanej, instrukcji) zajęło mniej niż 5 minut (i nie miało tu miejsca żadne „cudowne rozmnożenie” wyników 😉 ).
Pozdrawiam
AB
I jeszcze parę słów na temat pozostałych łamigłówek (w obu przypadkach potwierdzam zamieszczone już rozwiązania):
Jeśli chodzi o pierwszą, to można udowodnić, że nie da się uzyskać zamierzonego efektu ruszając tylko 4 klepki: Jak już dokładnie wyjaśnił Alek, musimy przesunąć o jeden moduł w prawo dwie z trzech leżących poziomo po lewej stronie czerwonej linii. Ten ruch bezpośrednio spowoduje przemieszczenie dwóch klepek po prawej stronie. Czyli już mamy ruszone 4. A dalej zauważamy, że po wspomnianym przesunięciu, z lewej lub prawej ich strony (w zależności od tego, które dwie ruszyliśmy) powstają dwa puste pola 1×1, co powoduje konieczność przełożenia przynajmniej jeszcze jednej klepki, a zatem łącznie co najmniej 5.
Jeśli zaś chodzi o drugą, to oparłbym się na spostrzeżeniu, że ze względu na powstające „zęby” nigdy nie uda się nam ułożyć prostokąta (o boku większym od jednego modułu), w którym byłoby więcej płytek 1×1 niż 1×2.
Przykładowy optymalny układ dla pomieszczenia 3×3:
1 22
22 1
1 22
Stąd wniosek, że płytki 1×1 maksymalnie mogą zająć 1/3 powierzchni, a więc 8*5/3= 13 1/3. Największą liczbą całkowitą jest zatem 13, ale ponieważ liczba ta musi być parzysta to w efekcie otrzymujemy 12.
Pozdrawiam
AB
„Drobiazgi” Sławka:
1. Jedno rozwiązanie podstawowe:
380*918=4*1*5*6*2907
+ wszystkie permutacje 4,5 i 6.
2. Dwa rozwiązania:
305*840=74+26*9851
518*401=70+32*6489
Oczywiście tym razem nawet nie próbowałem „na piechotę”, bo skończyłbym chyba po miesiącu. 🙂
Pozdrawiam
AB
Andrzej69:
„I tu pytanie do Pana jako autora, jak również do innych ?główkołamaczy?: Czy istnieje na to jakaś sprytna, chociaż może trudna do odkrycia, metoda, dzięki której rozwiązanie przychodzi szybko? Czy też pozostaje tylko wyjątkowo żmudna analiza ?kawałek po kawałku?, jak to było w moim przypadku?”
Moim zdaniem nie ma prostej metody. Rozpisując mnożenie w postaci „słupka” ujawnia się tylko trzy zera w iloczynach cząstkowych oraz wskazuje trzy cyfry, ktore muszą być parzyste i dwie nieparzyste. Dalej pozostaje, niestety, „droga przez mękę”.
Bardzo dziękuję Panie Marku za odpowiedź.
Wychodzi na to, że w sumie to postępowałem tak samo (nie bardzo tylko widzę tę drugą nieparzystą cyfrę, ale to, myślę, szczegół).
Generalnie chodziło mi o to, czy nie było tu jakiegoś triku, którego nie zauważyłem, a pozwalającego na stosunkowo szybkie osiągnięcie celu, podczas gdy ja przedzierałem się przez to „jak głupi” ;-). Ale z Pańskiej odpowiedzi wynika, że to jednak rzeczywiście jedyna możliwość (dzięki czemu mam trochę spokojniejsze sumienie 🙂 ).
Pozdrawiam
AB