Plaster antymagiczny

17 kwietnia 2016
Marek Penszko

Sześciokąt magiczny, jaki jest, każdy widzi:

Plan_bis

Jego magia podobna jest do tej, która rządzi kwadratami magicznymi. Konkretnie polega na tym, że do a(n)=3n^2-3n+1 komórek sześciokąta, a ściślej – sześciokątnego plastra (n to stopień plastra równy liczbie komórek wzdłuż jego boku), wpisane są wszystkie liczby od 1 do a(n) tak, że w każdym z 3r rzędów pól (po r=2n-1 poziomych, lewo- i prawoskośnych) ich suma S(m), zwana magiczną, jest taka sama.
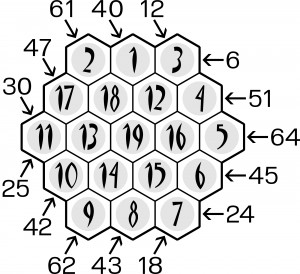
Obiekt na powyższym rysunku to jedyny istniejący (z dokładnością do obrotów i odbić) sześciokąt magiczny  – unikat odkryty (utworzony) i opublikowany po raz pierwszy przez niemieckiego architekta Ernsta von Haselberga w 1889 roku. Jego „parametry”: n=3, a(n)=19, r=5, S(m)=38.

Odwróceniem magii jest antymagia: magiczna suma S(m) zmienia się w wiązankę antymagicznych sum S(a), czyli takich, z których każda inna być powinna 🙂 . Antymagicznych sześciokątów trzeciego stopnia jest multum – poniżej przykład ze wskazaniem wszystkich piętnastu różnych sum.

Plan_2

Z sześciokątną antymagią wiąże się poniższe zadanie – zmodyfikowana łamigłówka z 10. Mistrzostw Świata (Brno, 2001).

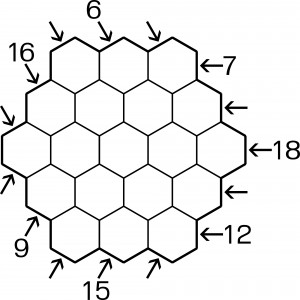
Plan_3

Do komórek sześciokąta należy wpisać liczby od 1 do 10 tak, aby powstał niepełny sześciokąt antymagiczny, zawierający po dwie liczby w każdym z piętnastu rzędów – dlatego właśnie niepełny (dziewięć pól pozostanie pustych). Siedem sum ujawniono; przypominam  – wszystkie sumy powinny być różne.

Kom