Bez słów
Sądząc po efektach zabawy indukcyjnej z poprzedniego wpisu, z większością moich gości rozumiemy się bez słów. Wystarczy rzut oka na przykład i wszystko jasne. Czasem tylko trzeba się poprzyglądać nieco dłużej.
Gwoli ścisłości, we wspomnianym zadaniu z nieskończonością poza regułą dotyczącą reszty z dzielenia sąsiednich liczb obowiązuje jeszcze jedna: cyfry w wierszach maleją od lewej do prawej (cyframi w kolumnach nie rządzi żadna dodatkowa zasada).
Prawdopodobnie przecieramy nowy szlak. Nie przypominam sobie, aby przed Łamiblogiem pojawiały się gdzieś łamigłówki indukcyjne, a ściślej takie, w których indukcja zastępuje instrukcję. Przeciwnie, raczej w modzie jest przesadna dbałość o to, by w opisie nie było żadnych niedomówień lub dwuznaczności. Zwłaszcza śmieszy mnie, gdy obok różnych odmian sudoku do znudzenia przypominana jest w całej okazałości podstawowa zasada. To trochę tak, jakby obok krzyżówki umieszczać informację, że wyrazy trzeba wpisywać w określone poziome i pionowe rzędy pól, umieszczając po jednej literze w każdej kratce. A tu proszę, można całkowicie usunąć opis i żadnych wątpliwości nie będzie, jeśli tylko przykład jest dostatecznie „wymowny”.
Indukcja w rozrywkach umysłowych kojarzy mi się głównie z kilkoma grami, z których chronologicznie pierwszą była Eleusis, karcianka opracowana przez Roberta Abbota przed ponad półwieczem. Parę innych gier jest do niej zbliżonych, a większość pozostałych to proste zabawy, w których chodzi o ustalenie jakiejś reguły postępowania na podstawie zachowania się lub reakcji graczy albo jednego z nich, zwanego „mistrzem”. Indukcja przydaje się także w niewielkim stopniu w wielu grach nieindukcyjnych, np. w pokerze.
Jedyna znana mi łamigłówka indukcyjna spoza Łamiblogu pojawiła się kilka miesięcy temu jako produkt komercyjny. Za jej rozwiązanie można zgarnąć okrągłe 1000 funtów brytyjskich. Powrócę do tego tematu w jednym z najbliższych wpisów. Pośpiechu nie ma, bo czasu na rozwiązywanie zostało jeszcze przeszło pół roku. A może ktoś z Państwa wie, co mam na myśli?
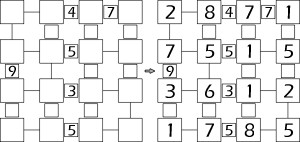
I już milknę, bo pora na eksperyment potwierdzający, że rozumiemy się bez słów. Niechaj przemówi przykład, a do akcji wkroczy indukcja. Rozszyfrowanie zasad nie wydaje mi się trudniejsze, niż poprzednio – zapowiadany twardy orzech pojawi się następnym razem. Natomiast samo zadanie, czyli skorzystanie z rozszyfrowanych reguł, chyba nie będzie takie łatwe.
PS Osobę, która jako pierwsza uporała się z zadaniem z nieskończonością, proszę o wybór nagrody (jednej z gier – Set!, 6. bierze lub Hive albo książki Łamigłówki. Podróże w krainę matematyki rekreacyjnej) oraz podanie adresu, pod który ma być wysłana. Informacje te proszę przesłać jako komentarz do niniejszego wpisu (nie będą ujawnione).
PS2 Jak słusznie zauważył pixl w komentarzu (ukryty do 22.07) przykład jest niejednoznaczny: w zadaniu brakuje jednej cyfry, ale niech tak zostanie – będzie dodatkowe zadanie:).


Komentarze
Panie Marku, nie wydaje mi się, by wszystkie reguły pasowały, w pierwszej kolumnnie przykładu: 2( )7(9)3( )1 powinno być 2( )7(9)3(3)1.
Jest to jedyny wiersz nie pasujący do reguł moim zdaniem (jeśli dobrze odgadłem reguły oczywiście:)
P.S. sugeruje to wynik dwucyfrowy co kłóci się na przykład z pierwszym wierszem, gdzie wynik jest jednocyfrowy, oraz z drugim, trzecim i czwartym gdzie jest liczba dwucyfrowa.
🙂 Hmm, Panie Marku wycofuję swoje komentarze:) już zrozumiałem w czym rzecz do końca, już wiem po co te puste kwadraciki:):):):)
A jednak, może to zbyt wczesna pora, ale wydaje mi się, że w zadaniu jednak jest błąd, przykład wydaje mi się, że rozpracowałem, ale w zadaniu moim skromnym zdaniem jest jakiś błąd, zajmę się tym później bo już czasu nie mam, i jak nie zobaczę żadnych poprawek dziś po południu to uznam, że błędu nie ma i wtedy moje rozumowanie jest błędne :):)
1 7 4 9 9 8
2 5 8 1 1 6
1 1 6 8 1 4
2 5 5 1 3 1
4 1 4 9 2 4
1 1 9 7 6 4
rozwiązanie rzędami:
1,7,4,9,9,8
2,5,8,1,1,6
1,1,6,8,1,4
2,5,5,1,3,1
4,1,4,9,2,4
1,1,9,7,6,4
P.S. przykład niestety nie sugeruje jednej reguły, że między kwadratami jest ostatnia cyfra ilorazu (jeśli prawdziwe jest moje rozwiązanie).
Duże kwadraty połączone ze sobą liniami tworzą większe liczby (dwu lub trzycyfrowe). Cyfry w małych kwadratach to wynik dzielenia obu liczb występujących obok danej cyfry. Puste małe kwadraty oznaczają, że dwie liczby da się podzielić bez reszty (można w nie także wpisać liczby, ale wzorując się na przykładzie nie jest to konieczne). Po rozwiązaniu zagadki okazuje się, że wynik dzielenia dwóch liczb w pustym małym kwadracie może być liczbą dwu lub nawet trzycyfrową. Inaczej mówiąc pusty mały kwadrat oznacza, że jedna liczba jest podzielna przez drugą.
A oto rozwiązanie:
1 7 4 9 9 8
2 5 8 1 1 6
1 1 6 8 1 4
2 5 5 1 3 1
4 1 4 9 2 4
1 1 9 7 6 4
W moim przypadku większy problem sprawiło znalezienie samej zasady niż rozwiązanie zadania.
Witam. Dziękuję bardzo za książkę i dedykacje 🙂 Pozdrawiam – MW.
28:4=7, 7:7=1
75:5=15
36:3=12
17×5=85(większa :a=mniejsza, mniejszaxa=większa, a-mały kwadracik)
1×7=7,7×7=49,49×2=98
2×29=58,58×2=116
1×168=168,168:12=14
25:5=5,5:5=1,1×31=31
41×12=492,492:123=4
1×19=19,19×4=76,76:19=4
174998
258116
116814
255131
414924
119764
Liczby w małych kwadratach mówią ile razy jedna z liczb jest większa od drugiej (liczby wielocyfrowe są połączone kreskami). Jeśli mały kwadrat jest pusty, to jedna z liczb jest dzielnikiem drugiej.
Zastanawiam się, czy jest jeszcze jakaś zasada, bo uwzględniając tylko to, podany przykład jest niejednoznaczny (w ostatnim rzędzie może być 1155 zamiast 1785)
Witam
Wydaje mi się że reguły sa nastepujące:
cyfry nie oddzielone małym kwadratem (pustym lub z inna cyfrą) tworza liczby;
liczby w małych kwadratach pomnożone przez mniejszą z liczb, z którymi się stykają dają większą liczbę;
puste małe kwadraty rozdzielają liczby z których mniejsza jest podzielnikiem wiekszej
Po wyindukowaniu powyższych zasad rozwiązanie zadania nie jest zbyt trudne.
rozwiązanie:
174998
258116
116814
255131
414924
119764
pozdrawiam
peha
Małe kwadraty oddzielają liczby o podanym ilorazie (wyniku dzielenia większej liczby przez mniejszą). Do diagramu należy wpisać cyfry od 1 do 9 (bez zera). W małe puste kwadraty można wpisać dowolne liczby naturalne (wynik dzielenia musi być jednak zachowany)
Rozwiązanie:
174998
258116
116814
255131
414924
119764
No mnie dłużej zajęło wymyślenie zasady niż wypełnienie.
174998
258116
116814
255131
414924
119764
Po dopisku do zadania w „PS2” znalazłem 2 dodatkowe rozwiązania przykładu różniące się
tylko ostatnim wierszem, zamiast:
1,7,8,5
można wstawić:
1) 1,2,6,0
lub
2) 1,4,7,0
rozwiązanie to
1 7 4 9 9 8
2 5 8 1 1 6
1 1 6 8 1 4
2 5 5 1 3 1
4 1 4 9 2 4
1 1 9 7 6 4
pzdr
Oprócz tych które podał Wiąz jest jeszcze jedno dodatkowe rozwiązanie w przykładzie.
W ostatnim wierszu można wpisać jeszcze:
1 8 9 0
Inne rozwiązania przykładu, podane przez Wiąza i Pitera, uwolniłem wcześniej – nie bez powodu…
m
Czyżby uwolnienie rozwiązań przykładu Wiąza i Pitera wiązało się z dodatkowym punktem zasad: należy użyć cyfr od 1 do 9.
Tak, choć to jakby dmuchanie na zimne, gdyby ktoś postanowił wypełnić diagram wyłącznie zerami albo pisać liczby zaczynające się zerem.
m