Twarde drzewa
Posadzić 8 drzew w 7 rzędach tak, aby był 1 rząd z 4 drzewami i 6 rzędów po 3 (nie więcej) drzewa w każdym.
Rozwiązania ogólne (topologicznie różne) są dwa:
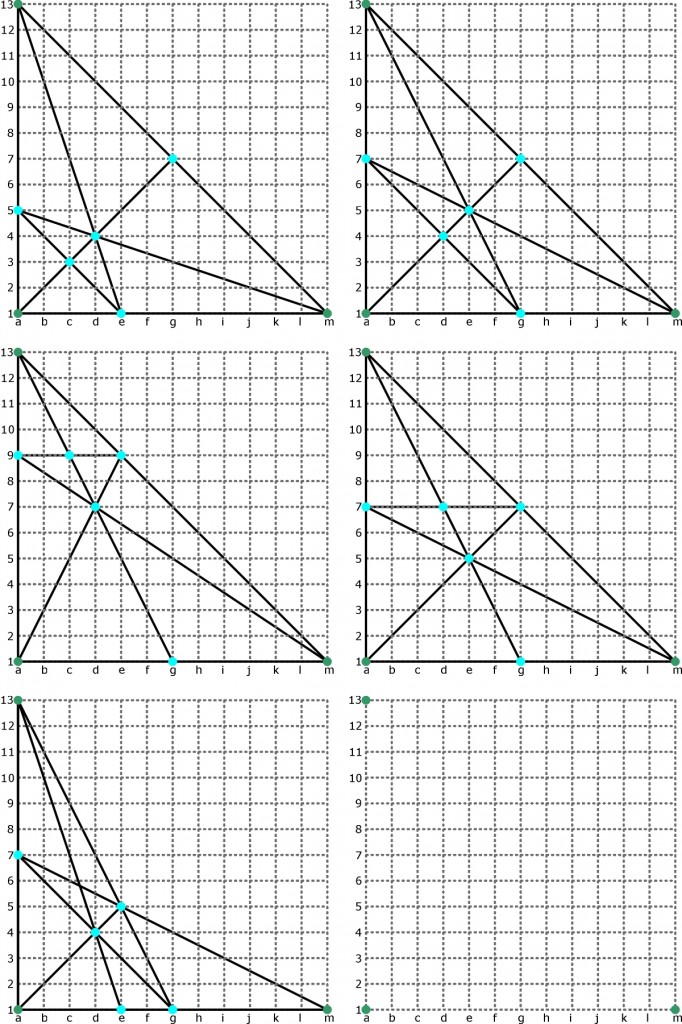
Szukanie rozwiązań jest trudniejsze, gdy drzewa rosną w węzłach siatki kwadratowej. Taką właśnie formę miało to zadanie w poprzednim wpisie, ale dla ułatwienia 3 drzewa były już ulokowane w rogach siatki, obejmującej kwadrat złożony ze 169 węzłów. Okazało się, że 5 pozostałych drzew można rozmieścić na pięć sposobów (jednego z nich, nadesłanego przez jawę i Wiąza, wcześniej nie znałem):
Jak widać pierwsze cztery sposoby odpowiadają pierwszemu rozwiązaniu ogólnemu, piąty – drugiemu.
Czy któreś z dwóch rozwiązań ogólnych tego zadania można, sadząc drzewa w węzłach, „wpasować” w prostokątny fragment siatki kwadratowej, obejmujący mniej niż 169 węzłów?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.


Komentarze
Jak na razie w 100 węzłach:
a1, b4, c3, d(2,4,10), g7, j4
81 węzłów:
a1, c5, d4, e(3,5,9), g7, i5
Pierwsze rozwiązanie zmieści się w siatce kwadratowej 6×6.
Punkty węzłowe (0,0);(0,3);(0,6);(3,3);(4,2);(4,3);(4,4);(6,3)
Drugi układ można umieścić w siatce prostokątnej 12×6.
Punkty węzłowe A(0,0);B(0,12);C(2,6);D(3,3);E(6,3);F(9,3);G(4,4);H(6,6)
Nie wiem czy nie ma mniejszych powierzchni.
Antypie, coś tu nie gra:
rzędy po 3 – DEF, BEG, BFH
rząd 4 – ADGH
trochę przymało rzędów po 3 albo czegoś nie widzę 🙁
mp
PS dla pierwszego sposobu siatka może być jeszcze mniejsza niż 6×6 (a właściwie 7×7 węzłów).
49 węzłów:
a4, c(3,4,5), d4, g(1,4,7)
35 węzłów:
a3, d(2,3,4),e3,g(1,3,5)
A czy takie kombinacje i dywagację są przydatne w życiu codziennym?? Czy tylko teoria dla samej teorii?
I przydatne, i teoria. Przydatne jako forma relaksu (oczywiście, nie dla każdego), a w dodatku pożyteczne, bo główka pracuje.
Jeśli natomiast chodzi o bardziej konkretne korzyści dla jednostek lub ludzkości, to szanse są nikłe, ale są – jak zresztą w przypadku 90% matematyki.
mp
A czy w życiu codziennym można wymienić konkretne i wymierne korzyści płynące z:
1) malowania obrazów
2) czytania książek na temat filozofii
3) oglądania filmów
Tu jest rysunek wyjaśniający rozwiązanie drugiego układu
http://pokazywarka.pl/hj87hy/
Dzięki, teraz wszystko gra [C to (6,2) a nie (2,6)].
mp
Taki mały off-topic… ale nie zupełnie:) Panie Marku, może znane dla Pana, ale jako że jest Pan miłośnikiem szachów, pozwolę sobie tutaj podesłac linka do czegoś, co ostatnio znalazłem:
http://www.gamesfanatic.pl/2012/04/17/schachen-czyli-szachy-bez-planszy/
Dzięki za info. Wygląda na fajną zabaweczkę. Spróbuję pograć zwykłymi figurami na kafelkach terakoty.
mp
😀 albo kafelki takie malutkie, albo ma Pan figury olbrzymich rozmiarów 😉
Płytki są normalne, ale każda jest podzielona na 16 mniejszych, więc w sumie wygląda to tak, jakby terakota była ułożona z małych kafelków.
mp
Np. a1,d1,g1,d4,c5,d5,f5,d7
Omyłeczka, nie f5 tylko e5