Piłowanie czekolady
Aby zapewnić rocznemu bobasowi (i sobie) dobrą zabawę, wystarczy dać mu czekoladę i święty spokój. Po kilkunastu minutach mamy widowisko – uradowane, brązowe dziecko i przerażoną jego wyglądem mamę.
Od paru dni czuję się jak brzdąc umorusany czekoladą – zgłębiam temat „łamanie czekolady, a łamanie głowy”. Podążam tropem wskazanym w komentarzu przez Michała, który wspomniał o książce Iana Stewarta Histerie matematyczne. Recenzowałem ją, ale prawie trzy lata temu – no i wyleciało mi z głowy, że jeden z rozdziałów dotyczył gier „czekoladowych”. Co gorsza nie mam jej pod ręką. Na szczęście jest to zbiór artykułów zamieszczanych wcześniej w Scientific American, a więc także w Świecie Nauki, polskiej edycji amerykańskiego miesięcznika – a te mam na CD. Artykuł ukazał się przed 12 laty.
Stewart opisuje dwie proste formalnie gry matematyczne, czyli takie, w przypadku których ciekawsze jest analizowanie strategii, niż granie. Myśl przewodnią można wyrazić sloganem: „prawie robi wielką różnicę”, bo reguły gier są prawie identyczne, a strategie krańcowo odmienne.
Mamy podzieloną rowkami na kostki tabliczkę czekolady. W pierwszej grze dwaj amatorzy łakoci odłamują na przemian po jednym kawałku w typowy sposób, od brzegu do brzegu – trrrach! – i do buzi. W drugiej grze prawie wszystko jest tak samo poza niezwykłym sposobem „odłamywania”: wskazuje się punkt na przecięciu rowków i wycina kawałek piłą do czekolad 🙂 , tnąc najpierw od góry, a potem od prawej strony do wskazanego punktu (jeśli punkt jest na lewym lub dolnym brzegu, piła tnie oczywiście tylko w jednym kierunku). Po takim ruchu nie zjedzona, czyli przeznaczona do dalszych cięć, pozostaje część tabliczki z narożną dolną lewą kostką, która jest… czekoladką przeczyszczającą (u Stewarta jest z chrzanem, a bywa też zatruta). W obu grach ten, komu przypadnie ostatni ruch, polegający na skonsumowaniu tego przysmaczka – przegrywa.
Pierwsza gra ma zapewniającą zwycięstwo strategię trywialną, druga – nie wiadomo jaką, czyli koszmarną. Trywialna jest radą: odłam taki kawałek, aby pozostawić kwadratową tabliczkę. Stąd wniosek: jeśli przyjdzie ci odłamywać coś od kwadratowej, to możesz od razu zażyć kostkę na przeczyszczenie. Natomiast koszmarna strategia drugiej gry jest taką dlatego, ponieważ z jednej strony matematycy nie potrafią jej rozgryźć, a z drugiej wiadomo (dowód jest genialnie prosty – zresztą typowy dla gier, które muszą się zakończyć czyimś zwycięstwem), że rozpoczynający zawsze może wygrać.
Znane są proste sposoby na zwycięstwo w niektórych przypadkach, np. gdy tabliczka jest kwadratowa lub wąska (2 albo 3 rzędy). Wiadomo też, dzięki wsparciu komputerowemu, jakie ruchy gwarantują sukces na setkach tabliczek, a właściwie tablic, o innych, konkretnych wymiarach. Matematykom jak dotąd nie udało się jednak efektów cząstkowych przekuć na jeden wniosek dotyczący ogólnej strategii.
„Koszmarną” grę wymyślił matematyk i ekonomista amerykański David Gale na początku lat 70. minionego wieku, a spopularyzował Martin Gardner, który nadał jej nazwę Chomp, czyli skrzyżował czekoladę (CHOcolate) z chrupaniem i mistrzem (chaMP). Jeśli kogoś temat zainteresuje, bez problemu znajdzie w sieci chrupiące strony; podane są np. w Wikipedii. A dla zachęty proponuję proste zadanie.
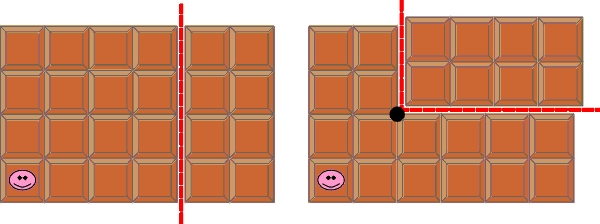
Gracze mieli smak na tabliczkę 5×6 – nastąpił pierwszy etap (dwa ruchy) konsumpcji i połowa drugiego:
Jaki powinien być drugi ruch drugiego gracza (proszę wskazać miejsce czarnej kropy, czyli punkt zasięgu piły), zapewniający mu zwycięstwo? 😉
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.


Komentarze
Hmmm…. Panie Marku sam Pan chyba dał rozwiązanie tego zadania, a przynajmniej wielki skrót do rozwiązania:
„Znane są proste sposoby na zwycięstwo w niektórych przypadkach, np. gdy tabliczka jest kwadratowa lub wąska (2 albo 3 rzędy).”
Stawiam na b2, ale chyba każdy punkt nie leżący na krawędzi ‚a’ oraz ‚1’ jest dobry….. chyba 🙂
Stawiam na d2.
Antypie, gram dalej:
1. d2 e1
2. ?
b2
Wiązie, rozumiem, że b2 to kontynuacja rozgrywki.
Po moim drugim ruchu całość będzie wyglądać tak:
1. d2 e1
2. b2 a5
3. ?
już widzę, że przegrałem 🙂
Ja po
1. d2 e1
zagrałbym
2. a3 …
Moim zdaniem wygrywa e1
Witmanie, po 2. a3 oczywiście wygrałeś!
A gdybym zagrał:
a) 1. d2 d1 2. …
b) 1. e1 d1 2. …
czyli w obu przypadkach pojawia się taki sam kształt?
mp
To wtedy zagram
2. b4
Tak jest!
Nie mam innego pomysłu na atak:)
mp
PS skuteczną odpowiedzią na ruch Antypa (d2) jest b3.
Nie słyszałem wcześniej o tej grze, dlatego chciałem jej się bliżej przyjrzeć i poszukać jakichkolwiek prawidłowości w optymalnym postępowaniu graczy. Z całą pokorą potwierdzam przedstawioną o niej opinię. Nie miałem na tyle cierpliwości, aby wydedukować dla tej gry wygrywający ruch drugiego gracza. Natomiast pokusiłem się na napisanie programu sprawdzającego, czy dana pozycja należy do wygrywających, czy może do przegrywających. Po wykonaniu programu dla zadanej pozycji okazało się, że jedynym wygrywającym posunięciem drugiego gracza jest ruch przedstawiony przez Witmana tj. e1. Przedstawiona przez p. Marka gra należałaby do tzw. gier kombinatorycznych, gdyby nie jedna „mała” różnica. Otóż w grach kombinatorycznych wykonujący ostatni ruch z definicji wygrywa. Jest wiele takich gier, dla których to założenie pozwala znaleźć ogólną prostą strategię postępowania graczy. Zmiana tego jednego warunku powoduje, że z gier o względnie prostych strategiach powstają „koszmarne” gry o niezwykle skomplikowanej strategii albo, jak w przypadku Chompa, strategii w ogóle nieznanej.
Pozdrawiam,
jazz
Jazzie, ja również korzystałem z programu i podejrzewam że Witman też. Szukanie zwycięskiego ruchu „na piechotę” jest zajęciem benedyktyńskim, mimo że do rozgryzienia pozostał niewielki kawałek czekolady (stąd przymrużone oko po pytaniu na końcu wpisu).
Chomp także jest grą kombinatoryczną, zaliczaną do gier typu nim. Wystarczy uznać, że ostatnia kostka jest nie-do-wzięcia i wówczas reguły będą w zgodzie z definicją.
Pozdrav
mp
Próbę rozwiązania zadania rozpocząłem od ustalenia układów przegrywających. Później znalazłem ruchy po których drugi gracz bez problemu wygrywa. Pozostałe możliwości analizowałem rzeczywiście przy użyciu programu – MS Paint.
Zabronienie wzięcia ostatniej kostki rzeczywiście czyni Chompa grą kombinatoryczną. Ale gdzie ta „radość” jaką mamy po spożyciu kostki z „nadzieniem”. Również na polu teorii gier efekt jaki uzyskujemy jest zupełnie różny od efektu jaki powstaje po wprowadzeniu w Chompie zasady, że ten wygrywa, kto bierze ostatni.
Panie Marku, napisał Pan, że rozpoczynający zawsze może wygrać i że dowód tego jest genialnie prosty. Jakoś genialnie mnie zamroczyło i nie widzę tego dowodu. Czy mógłby Pan coś na ten temat napisać? Nie chodzi o zamroczenie, tylko o dowód!
Z góry dziękuję i pozdrawiam,
jazz
Jazzie, dowód jest (chyba, bo jest w artykule „pierwodruku”) we wspomnianej książce Iana Stewarta, ale wspomnę o nim przy okazji następnego wpisu, z następnym zadaniem, z następnej gry… jeśli mnie nie zamroczy 🙂
mp