Dwa w jednym

12 grudnia 2008
Marek Penszko

Moja przygoda z łamigłówkami zaczęła się bardzo dawno temu od zabaw słowno-literowych. Nadal zresztą układam krzyżówki i lubię grać w Scrabble, więc nic dziwnego, że mam słabość do „zagadkowych” słów. Gdy tylko trafię na jakieś dotąd mi nieznane, natychmiast staram się ustalić, co oznacza. Ostatnio na przykład poznałem znaczenie wyrazu ARTEFAKT. Cóż, jakoś wcześniej nie nadarzyła się okazja…

Dla odmiany Richard Feynman, bohater poprzedniego wpisu, twierdził, że jako wykładowca nie przywiązuje do słów-nazw niemal żadnej wagi. Ściślej, chodziło mu o różnicę między znajomością rzeczy z nazwy, a znajomością samej rzeczy. Parokrotnie przywoływał zdarzenie z dzieciństwa, gdy ojciec pokazał mu jakiegoś ptaka, wymienił jego określenia w kilku językach i rzekł: „choćbyś poznał jego nazwy we wszystkich językach, absolutnie nic nie będziesz wiedział o tym ptaku”. Nic dziwnego, że Feynman nie przepadał za krzyżówkami, bo w nich prym wiodą słowa, a towarzysząca im wiedza jest szczątkowa.

Ponad rok temu zetknąłem się z wyrazem FUZULI. To nazwa całkiem zgrabnej łamigłówki wymyślonej w Turcji na fali rozrywek posudokowych. O istocie łamigłówki zapomniałem, o nazwie nie, bo wówczas spędziłem trochę czasu próbując wyjaśnić, co oznacza. Zresztą nadal nie wiem, jak powiązać znaczenie tego słowa w języku tureckim (niepotrzebny, zbędny) z istotą zadania, które określa. Jest wprawdzie jeszcze XVI-wieczny poeta Fuzuli, uznawany w Turcji za jednego z najwybitniejszych, ale raczej nie nazwałbym łamigłówki „Kochanowski” lub „Dantyszek”.

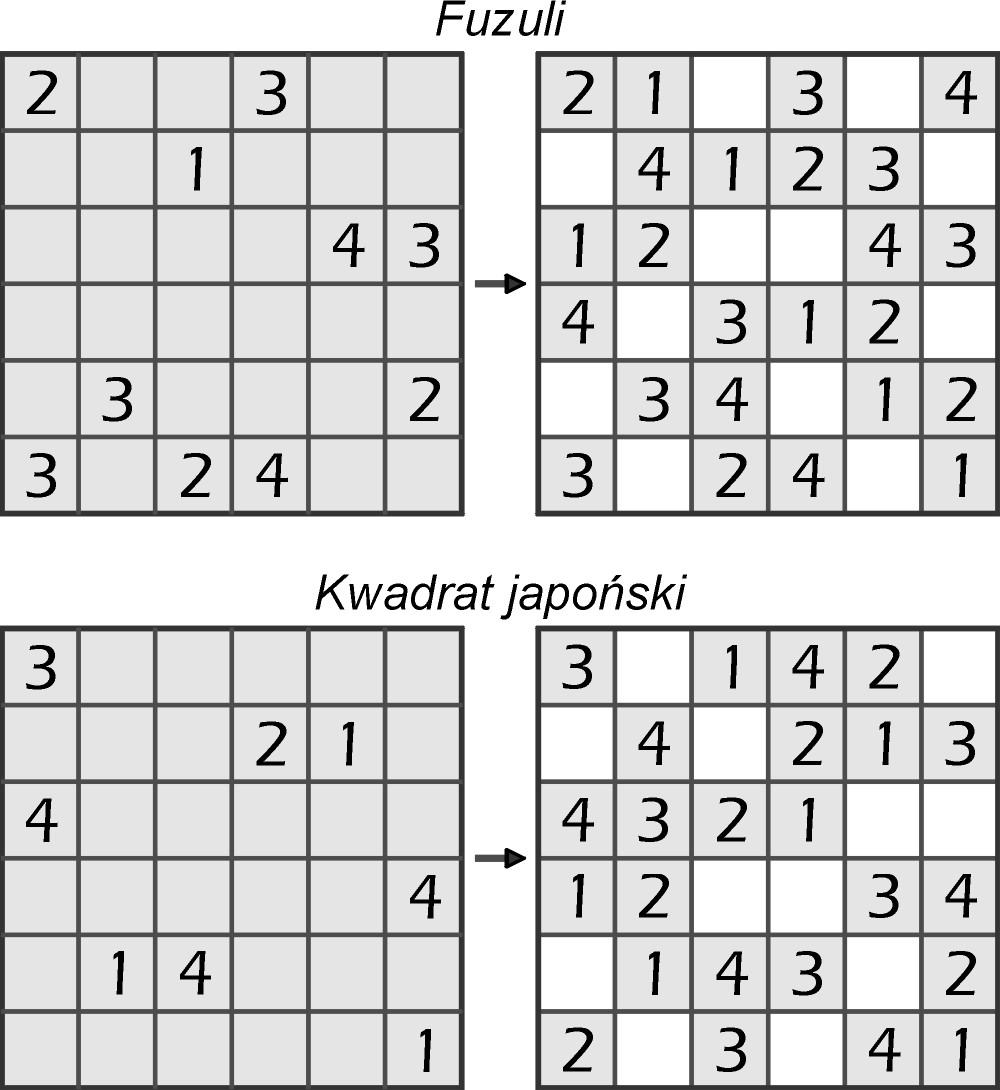
Fuzuli ponownie wypłynęło przed tygodniem, gdy przygotowywałem wpis dotyczący kwadratu japońskiego, czyli łamigłówki, której reguł wówczas nie znałem. Równocześnie wśród zadań zamieszczonych w internetowym konkursie zorganizowanym 6 grudnia przez Vladimira Portugalova zobaczyłem Fuzuli i przez chwilę miałem wrażenie, że to bliźniak mojego kwadratu japońskiego. Proszę porównać przykłady obu zadań i rozwiązania.

Nie znając reguł można by uznać, że to dwa zadania tego samego typu. Tymczasem wspólne jest w nich tylko to, co „łacińskie”: w każdym rzędzie i w każdej kolumnie kwadratu powinno znaleźć się n różnych cyfr (w przykładach n=4). Dalej jest inaczej.
Fuzuli: cztery cyfry nigdzie nie mogą znaleźć się w czterech kratkach tworzących kwadrat 2×2.
Kwadrat japoński (w wersji jak na powyższym przykładzie i w poniższym zadaniu): bezpośrednio nad (pod) cyfrą x nie można wpisać cyfry mniejszej (większej) od x.
A teraz pora na tytułowe dwa w jednym. W jakim sensie poniższe zadanie jest „2 w 1”, to także zagadka, choć tylko mini. Wypada jeszcze dodać, że n=5.