Skarby parami

6 września 2011
Marek Penszko

Bardzo lubię skarby, czyli łamigłówkową wersję komputerowego sapera. To klasyka wysokiej próby – wzorcowy, wręcz szkolny przykład wnioskowania dedukcyjnego. Na dłuższą metę oczywiście sztampa, jak każdy rodzaj łamigłówki serwowany w nadmiarze, ale urokliwa i zaraźliwa. Można wpaść w nałóg podobny do tego, który dopadał amatorów sudoku – znam przynajmniej kilka osób, które do dziś z nałogu się nie wyleczyły i w wolnych chwilach „pokątnie” wpisują cyfry w kratki.
Saperowi i skarbom poświęciłem przed trzema laty serię wpisów zaczynającą się tu, ale nadarza się okazja, by do tematu powrócić. Tureccy główkołamacze od roku serwują nową odmianę skarbów, formalnie nieznacznie różniącą się od wersji klasycznej, ale „nieznacznie” robi sporą różnicę w rozwiązywaniu. Sprawia, że wnioskowanie staje się bardziej zawiłe, więc wymaga intensywniejszego ruszania głową.

Zacznę od przypomnienia klasyki:

Cyfra w danym polu oznacza, w ilu sąsiednich kratkach – stykających się z polem z cyfrą bokiem lub rogiem – znajduje się skarb. W polach z cyframi skarbów nie ma. Należy oznaczyć wszystkie skarby (jak w małym przykładzie obok).
Wnioskowanie jest proste i piękne, rozwiązuje się jak po sznurku – szybko i przyjemnie.

Turecka nowość sprowadza się do krótkiego uzupełnienia reguł:
w kratce mogą znajdować się także dwa skarby.
Na przykład, skarby znajdujące się w polach otaczających cyfrę 2, mogą być umieszczone w dwu różnych kratkach lub w jednej. Zatem liczba możliwości ich rozmieszczenia wzrasta, co konkretnie i wyraźnie widać na prostym przykładzie, gdy cyfra jest w rogu diagramu:

Gdy A = 1, to możliwości jest tyle samo w klasyce (K) i nowości (N) – po 3.
Jeśli A = 2, wówczas K = 3, N = 6.
Gdy A = 3, to K = 1, N = 7.
Nietrudno zauważyć, że w związku z tym wnioskowanie dla N staje się bardziej „pokrętne” niż dla K. Zwięźle i obrazowo, choć niezbyt ściśle, można tę różnicę przedstawić tak:
W klasycznej wersji zwykle wnioskujemy:
A lub B; jeśli A to A1, jeśli A1 to A2: nie A2, więc nie A, czyli B.
W dwuskarbowym wariancie przeciętny ciąg wniosków staje się dłuższy i szerszy, czyli np.:
A lub B lub C; jeśli A to A1 lub A2, jeśli A1 to A1’… itd.
Krótko mówiąc, na poszczególnych etapach wnioskowania pojawia się więcej wariantów alternatyw do rozpatrzenia.

To, co napisałem wyżej, mogłoby znaleźć się we wstępie do propedeutyki teorii złożoności zadań logicznych. Warto by przy okazji rozważyć, co by się działo, gdyby pójść krok dalej i turecką regułę sformułować tak: w każdej kratce mogą znajdować się jeden, dwa lub trzy skarby. Właściwie należałoby zapytać, czy to miałoby sens, tzn. czy efektem byłaby jeszcze rozrywka, czy już pokuta, bo wariantów alternatyw pojawiłoby się tak wiele, a ciąg wniosków byłby tak długi i szeroki, że wnioskowanie logiczne zmieniłoby się w metodę prób i błędów.

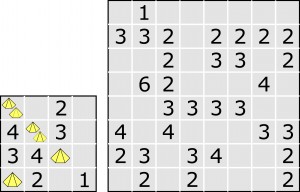
Wracając do alternatywy „jeden skarb lub dwa”, proponuję zmierzyć się z konkretnym zadaniem:

Mili podawacze rozwiązań proszeni są o wskazanie pól z dubeltowymi skarbami (na przecięciu których wierszy i kolumn są one?); pól do wskazania jest niewiele.

Oba zadania w tym wpisie pochodzą z tureckiego pisma „Akil oyunlari” (Gry logiczne); ich autorem jest Mehmet Murat Sevim.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.