M-5 i więcej
Nowojorskie muzeum dziecięce kusi od paru tygodni ekspozycją „Brain Teasers”. To nietypowa placówka, bo dotykanie eksponatów jest w niej wskazane, a w przypadku wspomnianej wystawy niemal obowiązkowe. Wbrew pozorom łamigłówki wcale nie są proste, natomiast ich forma jest zabawowa, a większość przypomina sztuki magiczne; wszystkie należą do klasyki. Taka prezentacja w erze gier komputerowych nieco trąci myszką, jednak dla milusińskich stanowi nie lada atrakcję. Stukać w klawiaturę i gapić się w monitor to nie to samo, co manipulować zagadkowymi przedmiotami lub wejść do środka układanki i mocować się z klockami nie tylko umysłowo, ale i fizycznie. Organizatorzy zapraszają, informując dla zachęty, że z jedną łamigłówką nikt się dotychczas nie uporał. Informacja jest półżartobliwa, bo od niemal dwóch wieków wiadomo, że rozwiązanie nie istnieje. Chodzi o lokal typu M-5, przedstawiony na poniższym rysunku.
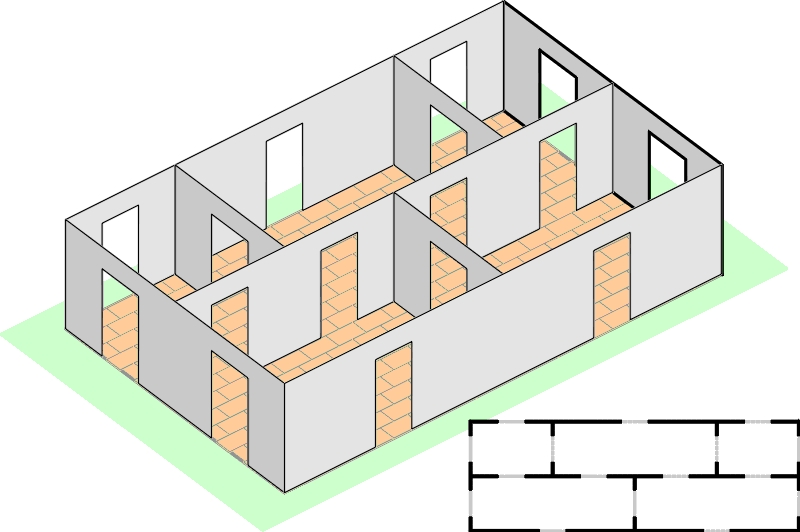
16 drzwi rozmieszczono w taki sposób, że dokładnie jedne są:
– w każdej zewnętrznej ścianie każdego pokoju;
– między każdymi dwoma sąsiednimi pokojami.
Trzeba zacząć wędrówkę w dowolnym miejscu i przejść przez wszystkie drzwi, przez każde dokładnie raz.
Dzieci i nowicjusze mogą się sporo nachodzić, zanim dojdą do wniosku, że jeżeli nie jest się duchem przechodzącym przez ściany, to szkoda nóg. Zawsze przynajmniej jedne drzwi pozostaną nietknięte.
Jak najprościej i najszybciej, czyli bez wędrowania lub rysowania czegokolwiek, można sprawdzić, czy tego typu wielopokojowe i wielodrzwiowe zadanie da się rozwiązać? – to pierwsza zagadka, łatwa.
Jak niemal wszystkie klasyczne zadania, także i to doczekało się wariacji na temat. Poniżej jedna z nich, nieco zakręcona.

Pokoi jest o dwa więcej (M-7), a drzwi aż 22, ale przez wszystkie za jednym zamachem również przejść nie sposób, więc dokładnie dwoje można pominąć. Natomiast wędrować trzeba tak, aby przechodzić na przemian przez drzwi oznaczone liczbą parzystą i nieparzystą. Ponadto trasa nigdzie nie może przecinać samej siebie.
Poniżej przedstawione jest jedno rozwiązanie – marszruta oraz odpowiadający jej ciąg liczb.
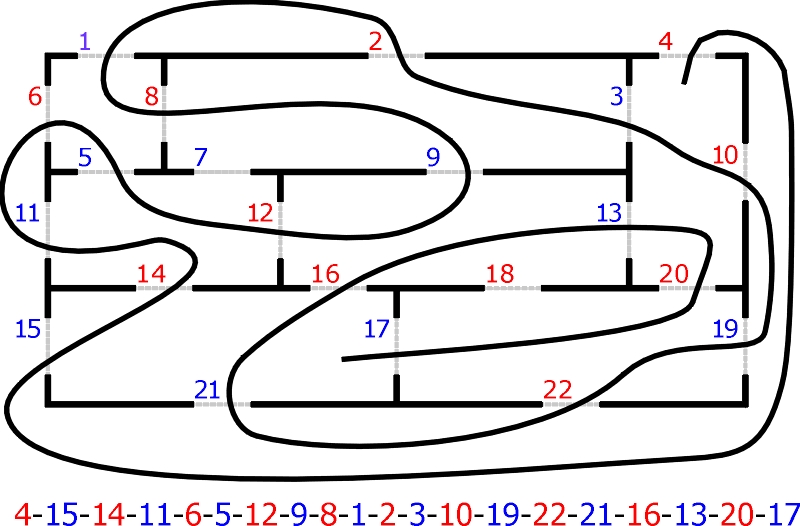
Czy uda się Państwu wyznaczyć inną drogę, zwłaszcza taką, która będzie miała z powyższą jak najmniej wspólnych fragmentów.
Na zakończenie niespodzianka (zapewne nie dla wszystkich): zadanie z lokalem M-5 ma jednak rozwiązanie, ale w pewnych szczególnych „okolicznościach”. W jakich – o tym następnym razem.

Komentarze
Z innej beczki, czy ktoś bawił się Eternity II? I czy ktoś używał Tetravex II? Czy jest przydatne? A może ktoś się już chwalił rozwiązaniem?
Panie Marku, czy w tym roku Polityka organizuje jakieś zawody sudoku?
Witam Panie Pawle,
niestety, Polityka już się nie bawi w łamigłówkowe „imprezowanie”. Turnieje sudoku i łamigłówek (ogólne) organizuje Sfinks.
Pozdrawiam
mp
Najprostszy według mnie sposób na przekonanie się o braku rozwiązywalności wielopokojowych zadań to sprawdzenie, ile jest pomieszczeń (wliczamy tu również otoczenie budynku) z nieparzystą liczbą drzwi. Takie pokoje mogą być co najwyżej dwa (w nich następuje początek i koniec trasy). Jeżeli jest ich więcej (jak w przedstawionym M-5), to zadanie nie ma rozwiązania.
Jeśli chodzi o drugą zagadkę, to możliwości jest oczywiście bardzo, bardzo dużo. Jedną z nich, formalnie różną od przedstawionej, możemy otrzymać przechodząc na końcu trasy przez drzwi nr 18 (zamiast 17). I zapewne między innymi dlatego sugestia, aby nowa trasa możliwie nie pokrywała się ze starą.
W związku z tym przyjąłem następujące założenia:
1. Zarówno początek jak i koniec ma miejsce w innych pokojach niż zaproponowano.
2. Każde przejście przez pomieszczenie (dotyczy to także części zewnętrznej) musi odbyć się inaczej niż w oryginale, np. wchodząc do małego kwadratowego pokoiku w lewym górnym rogu drzwiami nr 6, musimy go opuścić innymi drzwiami niż nr 5 i odwrotnie (tzn. wchodząc drzwiami nr 5 opuszczamy innymi niż nr 6). A bardziej matematycznie: jeżeli pewne dwie liczby sąsiadują ze sobą w ciągu pierwotnym, to nie mogą sąsiadować w ciągu wynikowym.
3. Wykorzystujemy oba wcześniej pominięte przejścia, natomiast opuszczamy któreś z wcześniej używanych.
Nawet przy tych założeniach rozwiązań jest z pewnością wiele, a jedno z nich wygląda tak:
3-13-9-2-4-10-1-6-19-8-16-15-21-17-22-11-5-8-7-12
Pozdrawiam
AB
Zwiedzanie muzeum dziecięcego nie tylko może być dużą atrakcją dla milusińskich, ale i niejeden dorosły chętnie pobawiłby się w takim muzeum.
Mam pewne uwagi do komentarza Andrzeja69:
1. Stwierdzenie o co najwyżej dwóch pomieszczeniach z nieparzystą liczbą drzwi może być nieco mylące i lepiej byłoby powiedzieć – „dokładnie dwóch pomieszczeniach z nieparzystą liczbą drzwi”.
2. Zaprezentowany przykład ciągu drzwi chyba się poprzestawiał w trakcie wpisywania, bo nie spełnia on jednego z założeń zadania – naprzemienności drzwi parzystych i nieparzystych.
Przykładowy ciąg mógłby wyglądać np. tak:
16-17-22-19-18-13-10-21-14-11-6-5-12-9-8-1-2-3-4-15,
ale, że jest to zadanie optymalizacyjne więc być może można znależć lepszy ciąg.
Dobry byłby np. taki ciąg:
12-11-2-9-16-15-10-13-18-19-4-3-8-5-14-17-22-1-6-21,
ale niestety ma on wielką wadę – nie lubi płaszczyzny.
Pozdrawiam
Spróbuję się ustosunkować do uwag Andrzeja, które niestety dopiero niedawno przeczytałem i dlatego też dopiero teraz na nie odpowiadam.
Jeśli chodzi o pierwszą z nich, to podtrzymuję stwierdzenie o co najwyżej dwóch pomieszczeniach z nieparzystą liczbą drzwi.
Dlaczego?
Otóż po pierwsze: może nie być w ogóle takich pomieszczeń – wówczas zadanie też jest rozwiązywalne: startujemy w dowolnym pokoju i kończymy w nim samym.
A po drugie: ponieważ drzwi zewnętrznych jest zazwyczaj dużo i trudniej je policzyć, możemy darować sobie otoczenie i sprawdzać wyłącznie pokoje. Możliwa jest wtedy sytuacja typu jeden pokój (drugim będzie sąsiedztwo budynku, ale tego nie sprawdzamy, bo po co). Tak więc liczymy wyłącznie pokoje z nieparzystą liczbą drzwi i jeśli jest ich 0, 1 lub 2 zadanie ma rozwiązanie (dlaczego przy tej metodzie nie obawiam się dwóch pokoi i otoczenia jednocześnie nie muszę chyba wyjaśniać).
Jeśli chodzi zaś o uwagę nr 2, to muszę Ci Andrzeju przyznać, że ująłeś to ładnie i dyplomatycznie, ale nazywając rzecz po imieniu, to rozwiązanie zostało przeze mnie totalnie skopane.
Prawda jest taka, że po prostu uciekł mi warunek o naprzemienności drzwi parzystych i nie. Zadania nie robiłem siedząc przy komputerze, a jedynie przeczytałem jego treść i wydrukowałem obrazki (w dodatku na czarno-białej drukarce, więc kolory przejść prawie nie różniły się), a do rozwiązywania usiadłem sporo później i zapomniałem o jednej z istotnych reguł (dziwiąc się za to, że takie łatwe 🙂 ). Najlepiej to widać choćby w stwierdzeniu, że najprostszy inny przebieg trasy to zamiana na końcu drzwi nr 17 na 18.
Dlatego też postanowiłem się poprawić i zastosować ściśle do reguł.
W tej sytuacji możliwych przebiegów jest oczywiście znacznie mniej, ale również sporo. W związku z tym, jak poprzednio, postanowiłem stworzyć trasę możliwie różną od przedstawionej, tzn. spełnić trzy założenia wymienione w moim wcześniejszym komentarzu.
I tu pewne zdziwienie: otóż nie da się w całości zastosować do żadnego z tych założeń! Jest to możliwe co najwyżej częściowo.
Dlaczego?
Na początku należy zauważyć, że wybór przejść, które moglibyśmy ominąć jest mocno ograniczony.
Wynika to z faktu, że w pokojach o nieparzystej liczbie drzwi zawsze dwoje z nich są jednego typu (np. parzyste), a troje – drugiego. Przejścia, które są w mniejszości musimy zaliczyć oba, możemy natomiast ewentualnie opuścić jedno z tych, których jest trójka. Jeśli teraz pod tym kątem przeanalizujemy wszystkie pokoje, to okaże się, że potencjalnych kandydatów do pominięcia jest raptem trzech: 7, 18 i 20. Nie możemy przy tym ominąć jednocześnie 18 i 20 (bo należą do tego samego pomieszczenia), a więc musimy zostawić zamknięte drzwi nr 7 (czyli tak jak w oryginale), co powoduje, że założenie nr 3 w całości spełnione być nie może.
Przyjrzyjmy się teraz pomieszczeniu w lewym dolnym rogu. Ma ono pięć drzwi i wszystkie one muszą być wykorzystane, a to z kolei oznacza, że właśnie w nim następuje początek lub koniec trasy. Znowu pokrywa się to z przebiegiem pierwotnym przecząc tym razem założeniu nr 1.
Ostatnie z założeń (nr 2) również w całości spełnione nie będzie, a zgodność z przykładową trasą nastąpi przynajmniej w pięciu miejscach. I tak: Oba odcinki przechodzące przez pomieszczenie położone w środku górnego traktu (istnieje tylko jeden zgodny z regułami sposób jego przejścia: 2-3 i 8-9), analogicznie jest z pokojem po lewej stronie środkowego traktu (odcinki 5-12 i 11-14), do tego dochodzi jeszcze jedno z zewnętrznych połączeń: 4-15 – każda inna próba jego poprowadzenia powoduje „odcięcie” po obu jego stronach różnej liczby drzwi parzystych i nieparzystych.
Reasumując: wytyczenie trasy całkiem różnej od zaproponowanej nie jest możliwe – drzwi nr 7 zawsze będą omijane, start (lub zakończenie) musi mieć miejsce w pokoju w lewym dolnym rogu, pięć odcinków można przeprowadzić w jeden jedyny sposób.
Teraz można postawić dwa pytania:
1. Czy nowa droga może się różnić od starej we wszystkich pozostałych miejscach? A jeśli nie, to w ilu punktach jeszcze muszą się pokrywać?
2. Jaki jest przebieg takiej optymalnej drogi?
Na pierwsze pytanie odpowiedź jest negatywna. Mimo, że każdy nowy odcinek (poza wymienionymi wcześniej) może być różny niż w oryginale, to zawsze jeszcze przynajmniej dwa będą zgodne z układem pierwotnym. Nie będę już tutaj przeprowadzał analizy – nie jest ona trudna, a za to dość kłopotliwa w opisie.
Jeśli zaś chodzi o pytanie drugie, to takie optymalne, czyli maksymalnie różniące się od oryginału (choć do siebie bardzo podobne), przebiegi są tylko dwa:
12-5-6-1-8-9-16-17-22-19-18-13-10-21-14-11-2-3-4-15
12-5-8-9-16-17-22-19-18-13-10-21-14-11-6-1-2-3-4-15
Jak widać różnią się one między sobą tylko momentem zaliczenia drzwi nr 1 i 6.
Poza wcześniej wymienionymi miejscami pierwszy z nich pokrywa się z pierwotnym na odcinkach 5-6 i 1-8, a drugi 11-6 i 1-2. O ile się gdzieś nie pomyliłem, to bardziej odmiennych tras przeprowadzić się nie da.
Mam nadzieję, że choć trochę udało mi się zrehabilitować. 😉
Pozdrawiam
AB
Czy mógłby pan podać mi rozwiązanie z m5
Rozwiązanie podałem we wpisie „Ku niewiadomej” 18 lutego.
mp
Dzięki
Ale po co tyle pisać wystarczy zbudować graf i zbadać stopnie jego wierzchołków i mamy odpowiedź bez żmudnego rysowania
nie prawda