Przedsmak 2
Pierwszy przedsmak był przed poprzednim, czyli tegorocznym wakacyjnym Omnibusem. Drugi poprzedza Omnibus zimowy, który – jeśli wszystko dobrze pójdzie – ukaże się w połowie grudnia. Przedsmakiem jest poniższe zadanie, a ściślej rodzaj zadania, szykowanego do tegoż Omnibusa.
Ponieważ jednak Łamiblog jest bardziej wyrafinowany niż Omnibus, więc i zadanie jest trudniejsze niż porcja szykowana na zimę – także dlatego, że nie zawiera instrukcji. Krótko mówiąc, stanowi dawno nie widzianą w Łamiblogu łamigłówkę indukcyjną. Podany jest tylko przykład z rozwiązaniem, z którego należy się domyślić, o co chodzi, a następnie uporać się z nieprostym zadaniem, korzystając z odgadniętych z przykładu reguł zabawy.
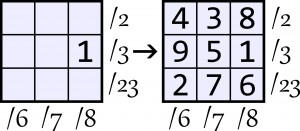
Przykład wygląda tak:
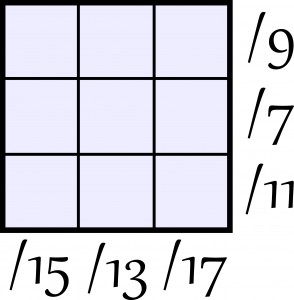
A zadanie tak:
Piszemy o tym, co ważne i ciekawe
Zniknięcie Anżeliki
Anżelika Mielnikawa, ważna białoruska opozycjonistka, obywatelka Polski, zaginęła. W lutym poleciała do Londynu. Tam ślad się urwał. Udało nam się ustalić, co stało się dalej.
Życzę przyjemnych i owocnych prób wpisania cyferek.

Komentarze
Do diagramu należy wpisać cyfry od 1 do 9, tak aby liczby powstałe w wierszach i kolumnach były podzielne przez liczby podane z boku diagramu.
927
483
561
Rozwiązanie jest jedno. Dla przykładu, na podstawie którego należy odgadnąć zasady, rozwiązań jest od groma. Przykład jest specyficzny, ponieważ jest kwadratem magicznym. Jedno z możliwych innych rozwiązań:
432
951
876
Poprawiłem przykład, aby było jedno rozwiązanie. Jest?
mp
Zadanie dość szybko sie robiło, ale przy założeniu, że nie ma zera:
lewy, dolny róg to 5 co daje tylko dwie kombinacje cyfr przy podzielności przez 9, a co dalej idzie tylko kilka liczb z podzielnością przez 11 (zaczynających się na 5 i nie mających cyfr z podzielności przez 9: 2 komplety cyfr).
I to dość szybko szło, ale na samym końcu nie wyszło :):)
Wniosek? Błędnie założyłem brak zera:(
Na drugie podejście już nie mam czasu
7,6,11
12,8,4
5,10,9
mam pewne wątpliwości, ale jak wiemy, należy je mieć.
Nie lubię łamigłówek indukcyjnych.
Tutaj jednak dość szybko wpadłem na trop:
w pola diagramu należy wpisać dziewięć różnych cyfr od 1 do 9, tak aby trzycyfrowe liczby utworzone w wierszach i kolumnach były podzielne przez odpowiednią liczbę podaną obok diagramu.
Przy takim założeniu zadanie ma jedno rozwiązanie (niestety znalazł je komputer i nie potrafię określić czy na piechotę pójdzie łatwo):
927
483
561
Natomiast zastanawia mnie fakt, że zadanie przykładowe ma przy takim określeniu reguł aż 4 rozwiązania i szczerze mówiąc brakuje mi pomysłów czy nie powinno być jeszcze jednej reguły. Oto rozwiązania:
348
195
276
438
951
276
498
315
276
932
156
874
Poprawiłem przykład tak, aby rozwiązanie było jedno (mam nadzieję, że jest).
mp
Tak, po wpisaniu w diagramie przykładowym jedynki rozwiązanie jest tylko jedno.
Komentarz oczywiście można usunąć po odczytaniu…
Pozdrawiam serdecznie
Proszę o komentarz w kwestii zmian w przykładzie;
bo nie wiem czy moje rozwiązanie i wątpliwości, które sygnalizowałem było ich przyczyną (?)
Zmiany wprowadziłem, aby rozwiązanie przykładu było jedynym możliwym. Przed zmianami (1 wpisane w diagram, 23 zamiast 4 obok diagramu u dołu z prawej strony) podane rozwiązanie przykładu było jednym z wielu możliwych.
mp
927
483
561
Po przyjściu z pracy miałem już chwile :
027
483
561
Punkt wyjściowy był jak w komentarzu poprzednim, z tym ze nie pomijałem juz zera
Powinienem uwolnić, bo jest błędne, ale nie uczynię tego, bo różni się tylko jedną cyfrą od prawidłowego. Byłoby OK, gdyby rozwiązanie bez zera nie było możliwe.
mp
Ha ha ha!
Dobre!
927
483
561
Przecież 9 tez jest podzielne przez 9.
czasem nie widać takich oczywistości
Rozwiązaniem jest:
927
483
561
A zasady? Jeśli dobrze je rozumiem, to poniższe również ma jedno rozwiązanie:
[_] [_] [_] /31
[_] [_] [_] /2
[_] [_] [_] /6
/8 /13 /7
837
954
612
Uff!
mp
Obok/poniżej diagramu podane są dzielniki liczb trzycyfrowych odczytanych w danym rzędzie/kolumnie.
W każdą kratkę wpisujemy inną cyfrę.
Ujawniona 15 pozwala od razu ulokować 5 w lewym dolnym rogu. Liczb podzielnych przez 11, różnocyfrowych, bez 0, mieszczących się w przedziale 500-600 jest 7 (każda kończy się inną cyfrą, żadna nie kończy się 6), natomiast liczb podzielnych przez 17 (trzecia kolumna), złożonych z różnych cyfr, bez 0 i 5 w jakimkolwiek miejscu oraz bez 6 w rzędzie jedności naliczyłam 14 (dwie z nich odpadają ponieważ zawierają cyfrę, która musiałaby się znaleźć obok wpisanej 5). Został okrągły tuzin możliwości z pięcioma wpisanymi cyframi…
A rozwiązanie wygląda tak:
9 2 7
4 8 3
5 6 1
927
483
561
Świetnie mi się rozwiązywało. Zasady od kopa, rozwiązanie zacząć od 5, później możliwe kombinacje dla 11, i dopasowanie liczb do \17 i \13 i voila
Pozdrawiam
Propozycja reguł:
1. W kwadrat wpisać liczby tak by powstał kwadrat magiczny.
2. Liczby utworzone wierszami i kolumnami mają być podzielne przez odpowiednie liczby /x (przykład, jeśli w wierszu jest 13,5,18 /9 to 13518 dzieli się przez 9)
Kwadrat magiczny w przykładzie występuje niejako przy okazji, więc warunek (1) jest zbędny.
mp
No i chyba jeszcze:
3. liczby tworzące kwadrat muszą być kolejne i najmniejsze z możliwych.
Jeśli przyjąć, że liczby to mają być cyfry ale za to mogą się powtarzać to może być np. tak:
126
364
506
Ale to chyba za proste
Zasady to oczywiście podzielność.
927
483
561
Ja też mam takie zadanie (łatwiejsze):
http://pokazywarka.pl/4gmis1/
927
483
561
Wierszami od góry: 927; 483; 561. Kolumnami od lewej: 945; 286; 731.
Chodzi o to, by wpisać różne cyfry od 1 do 9 (nie musi być kwadrat magiczny, jak myślałem na początku) i by utworzone z nich liczby w rzędach i kolumnach dzieliły się przez liczby po prawej, bądź na dole. Ten znak „/” jednak jest sporą podpowiedzią. Zaczynamy od stwierdzenia, że w lewym dolnym rogu musi być 5, i szukamy par 5xy dzielące się przez 11 i pqy dzielące się przez 17; par spełniających warunki jest 12. Następnie dobieramy np. poczynając od szukania wielokrotności 13, i w końcu odnosimy sukces; oczywiście wszystko z pomocą excela
927
483
561
Poprawiony przykład ma tylko jedno rozwiązanie. Gdyby w diagramie nie było wpisanej jedynki, to istnieją jeszcze trzy inne rozwiązania:
348
195
276
498
315
276
932
156
874
927
483
561
Zasady proste. Nie wiem jak innym ale mnie sprawdzenie czy nie ma wielu rozwiązań zajęło sporo czasu.