Ostrożnie z zapałkami
Czytelnicy ósmego Omnibusa przysyłają maile z uwagami. Najczęściej dotyczą one zapałczanek arabskich. Stara prawda, że z zapałkami trzeba ostrożnie, nabiera nowego znaczenia.
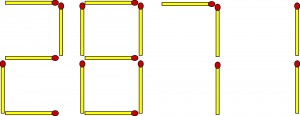
Na pierwszy ogień (od tego najbardziej się czerwienię) wezmę pierwszą część zadania D: liczbę 2871 należy zmienić w najmniejszą możliwą, przekładając dwie zapałki.
11-letni chłopiec przysłał rozwiązanie lepsze (mniejsza liczba) niż to, które podałem. Ciekawe, że żadna z kilku osób dorosłych, które poinformowałem o tym byczku i prosiłem o poprawienie rozwiązania, nie wpadła na to, które nadesłał jedenastolatek. To mnie trochę tłumaczy, ale nie usprawiedliwia. A Państwo wpadną? Liczby ujemne wykluczamy.
Zadanie G: Przemieszczenie dwóch zapałek prowadzi do prawidłowej równości.
Okazuje się, że rozwiązania są dwa (a może więcej?). Jakie?
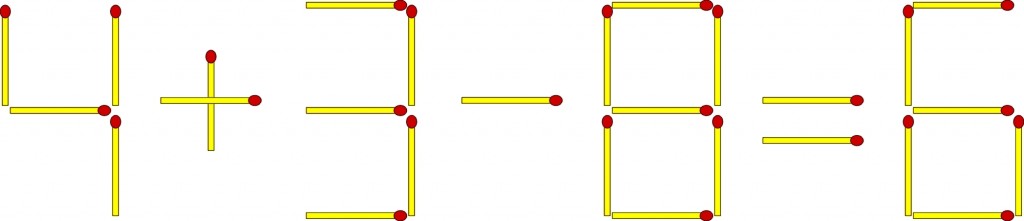
I na koniec istna eksplozja, czyli zadanie E: poprawna równość powinna powstać po przełożeniu dwóch zapałek.
Napisałem, że rozwiązania są dwa, a tymczasem… Obawiam się, że jeśli Łamiblogowicze wespół w zespół wezmą się za rozwiązywanie, to może paść nawet kilkanaście.
Komentarze
0071 się liczy?
Nie
mp
62+64=63*2, jedna przekładamy, jedna odrzucamy, czyli 2 przemieszczamy.
Odrzucanie odrzucamy
mp
zapomiałem dopisać drugie rozwiązanie:
63+63=63*2
pierwsze zadanie:
1287, przekładamy jedynkę z końca na początek 🙂
Zadanie D: 283? Nie widzę szans na lepszy wynik, może dwadzieścia lat wcześniej udało by się coś jeszcze urwać 🙂
Ten ósmy omnibus był w zeszłym roku:
2014?
no to jak nie 0071 to 2014
W zadaniu pierwszym mamy 283
Zadanie E: 9-3-0=6
Zadanie D. Czy można odwrócić liczbę do góry nogami?
Liczba 2871 od góry wygląda jak 1L82. Trzeba zabrać jedną zapałkę z L i jedną z 8, a potem obie przełożyć do 2. Otrzymuje się wówczas liczbę 1168.
Zadanie G. Lewą stronę równania można przerobić na 63+63, ale to pewnie zbyt oczywiste i trzeba poszukać czegoś wymyślniejszego 🙂
Obracanie do góry nogami to… chwyt poniżej pasa:)
63+63 jest jak oczywiście OK!
mp
87
Mniejszą liczbą jest 887
63+63=63*2
887 nie znałem, ale można mniej.
mp
PS co znaczy 87 na początku? Czy to wybrakowane 2187?
Zapałki z jedynki przekładamy do siódemki i robimy z niej trójkę. Rozwiazanie: 283.
1168 ??
Zadanie E. Równość można też uczynić prawdziwą po przełożeniu jednej zapałki. Jeśli się 4 przerobi na 11, to mamy 11 + 3 – 8 = 6.
Z lekkim przymrużeniem oka, ale w porządku (to rozwiązanie jest podane w Omnibusie przy jednozapałkowym wariancie zadania).
mp
😀 jasne!
283
Jak człek sie zafiksuje, to koniec!
Zadanie G:
Znalazłem dwa rozwiązania, więcej nie chce mi nic wyjść
62 + 56 = 59 * 2
63 + 63 = 63 * 2
Ha, pierwszego nie znałem – jest super!
W takim razie są trzy rozwiązania, ale powinienem dodać, że znaki działań też można zmieniać i dozwolone jest dzielenie w postaci ukośnej jednej zapałki (połowa znaku mnożenia), ale to chyba byłaby zbyt mocna podpowiedź.
mp
Dla równości C istnieje jeszcze jedno rozwiązanie 18-3=3*5
Super!
mp
Zadanie D. Najmniejsza możliwa liczba to 280 🙂
Ale jak? Bo jeśli przerobić dwie jedynki na „grube” zero, to będzie nawet 200.
mp
Zadanie E. Mam dwa rozwiązania:
4 – 3 + 8 = 9
4 + 2 + 0 = 6
Zadanie G. Bardzo ciekawe, tylko niestety uzyskane po przełożeniu 3 zapałek, jest rozwiązanie:
62 + 570 = 632
Cyfra 7 powstała z zapałek usuniętego znaku mnożenia, a cyfrę 0 zrobiono z 9.
Jak 7 zmieściło się między 5 a 0? Chyba wirtualnie.
mp
87 to pomyłka. Liczba najmniejsza to 283.
zadanie D, oczywiście można lepiej, likwidując jedynkę i przerabiając 7 na 3 co daje 283
D: Można by jedynkę zmienić w plusa i zapisać 28+7 czyli 35
G: 63+63=63*2
Zadanie G:
63+63=63×2
62+56=59×2
Zadanie E:
4+2+0=6
3+3-0=6
Zadanie D jest ponad moje siły 🙁
Rzeczywiście w zadaniu E znalazłem jeszcze
9-3-0=6
4-3+8=9
Mam! Rozwiązanie zadania D to 200.
Ale to z przymrużeniem oka (grubaśne zero). A poważnie?
mp
D: 1 do potęgi 287
G: 62+56=59×2 albo 63+63=63×2
E: 4-3+8=9
4+2+0=6
+1-3+8=6
4+9-8=5 (żeby były użyte dwie zapałki, jedną ze znaku „=” 3 uzupełniamy do 9, a z 6 jedna uzupełnia =)
9+3-6=6 (podobnie jak w poprzednim)
Ad 1.
200 wchodzi w rachubę?
Półżartem tak („grube” zero).
mp
62-59=63/21
63+63=126
Nie 280, tylko 283 miałam napisać. Jedynka (2 zapałki) idą do 7 i razem tworzą 3.
D: 283.
Na razie D:
1. pomysł: 283
2. pomysł: 28,11
E: 3+3-0=6
283!
D: 1108
(?) wspak?
mp
G: 63+63=63×2
E: 4+2+0=6
Jeszcze G: 62-59=63/21.
Zanim wpadłem na prawidłowe rozwiązanie, podobnie jak @stud to rozwiązałem, tylko, że nie 1108, a 1168 😉
I nie wspak, panie Marku, a do góry nogami! 😀
11 latek mógł wszak usiąść po drugiej stronie stołu 🙂
ale rozumiem, że w tym przypadku jest to niedozwolone, tak?
Generalnie w zapałczankach jest trochę luzu i żartu. W związku z tym, czy coś jest dozwolone, czy nie, pozostaje kwestią umowy. Proponuję, żeby obchodzenie stołu nie było dozwolone.
mp
D: 283
Przypomniało mi się bardzo ładne zadanie z zapałkami:
Dołóż jedną zapałkę, aby powstała prawidłowa równość:
100 + 510 = 200
A poważnie to 283 Panie Marku!
Miodziu, czy to ma być zapałka przekreślająca znak równości? 🙂
@miodziu: tak wydaje mi się, że wystarczy zamienić cyferkę na literkę 🙂
11+3-8=6
4+2+0=6
1+13-8=6
3+3-0=6
1 zapałka:
4+9-8=5
E: 4+2=6=6
Przy zadaniu D jeszcze jedna możliwość przyszła mi do głowy, tylko nie wiem, czy jest dozwolona. Zabieramy środkową zapałkę z 8, i robimy z niej przecinek po 2. A potem poziomą zapałkę z 7 przekładamy do 1. Otrzymujemy liczbę 2,017. Już niżej chyba się nie da 🙂
A w zadaniu Miodzia, to można by tą dodatkową zapałką zmienić znak równości na znak „większe równe”.
Przecinek to w kategorii „półżartem”
mp
Jakoś nie widzę 283 w odpowiedziach zad. D
Nie uwalniam od razu poprawnych odpowiedzi.
mp
9-3-0=6
4-3+8=9
Zadanie Miodzia byłoby trudne, gdyby nie druga część zadania D w Omnibusie. Zmieniając położenie jednej zapałki w 518 otrzymać jak najmniejszą liczbę. Rozw. STO
Plusy, znaki mnożenia i równości są w porządku, zatem znak dzielenia chyba też Pan uzna? 28\7, czyli 4. Zmieści się! Między 2 a 8 trudno by było podzielnik wsunąć, ale przed 7 wejdzie 🙂
Ot, spryciula:)
mp
D: 283
@OlaGM:
Miała powstać równość, a Tobie wyszła nierówność 🙂
E:
3+3-0=6
4+9-5=8
@miodziu:
dodatkową zapałką przekreślamy znak równości 😉
@miodziu:
Właśnie zauważyłem, że OlaGM wpadła na ten sam pomysł i dostała odprawę 🙂 więc cofam !!!
G: 63+63=63×2, 62+56=59×2
A teraz zadanie E. Najpierw 3 „normalne” rozwiązania:
4-3+8=9, 4+2+0=6, 9-3-0=6.
Równość 4+9-8=5 można uzyskać po przełożeniu jednej zapałki z szóstki do trójki. Można ją też uzyskać, przekładając którąś z pozostałych 26 zapałek na właściwe miejsce do trójki, a następnie w zwolnione miejsce niepotrzebną zapałkę z szóstki. Zatem przekładamy 2 zapałki. Takich sposobów mamy 26.
Równość 11+3-8=6 można też uzyskać, przekładając jedną poziomą zapałkę z czwórki, ale podobnie jak wyżej można to zrobić na 26 sposobów, przekładając 2 zapałki.
Razem mamy 3+2×26=55 sposobów (nie wiem, czy nie ma innych).
Gdyby u Miodzia + oznaczał dzielenie, zadanie byłoby dużo prostsze… Może tam na plusie jest taka zapałka z dwiema główkami (!) i ten znak naprawdę oznacza dzielenie?
Miodzio,
Doczytałem komentarz Antypa – świetne zadanie!
E: 9-3-0=6
G: 63+63=63*2