Cztery punkty
Wspominałem w jednym z poprzednich wpisów o sposobie rozwiązywania zadań opartym na tzw. „zjawisku aha!”, czyli wpadnięciu na pomysł. Oto jedno z klasycznych zadań, w przypadku których z reguły taki właśnie sposób jest skuteczny – stawiają one spory opór, dopóki rozwiązujący nie dozna… olśnienia.
Z sześciu zapałek należy ułożyć cztery trójkąty; zapałki nie powinny się przecinać, mogą tylko – i powinny – stykać się końcami.
Jeśli ktoś z Państwa nie zna tego zadania, zachęcam do rozwiązywania, ale proszę teraz przerwać czytanie, a przynajmniej nie sięgać wzrokiem dalej, niż do zamieszczonego poniżej pierwszego rysunku. Wprawdzie poniżej nie ma rozwiązania, ale jest coś, co może na nie naprowadzić, czyli nieco popsuć zabawę.
Łamigłówka ta czasem pojawia się w nieco innej, następującej postaci:
należy zmienić położenie trzech z sześciu zapałek tworzących dwa trójkąty (rysunek) tak, aby powstały cztery trójkąty. Zakaz krzyżowania zapałek pozostaje oczywiście aktualny.

Właściwie zabawa z zapałkami jest pretekstem do nieco innego tematu. Zauważmy, że gdyby trzy zapałki miały jednakową długość, ale były krótsze od trzech pozostałych, także równych między sobą, to przy odpowiednim dobraniu obu długości rozwiązanie byłoby trywialne i wyglądałoby na przykład tak, jak na poniższym rysunku z lewej strony.
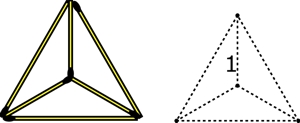
Spójrzmy teraz na to rozwiązanie nieco inaczej.
Końce zapałek wyznaczają cztery punkty, a długości zapałek odpowiadają wszystkim odległościom między parami punktów (na rysunku powyżej z prawej). Różne odległości są tylko dwie. Jeśli mniejszą przyjmiemy za jednostkę, to większa będzie wynosić sqrt3.
Czy można inaczej rozmieścić cztery punkty na płaszczyźnie tak, aby wśród sześciu odległości między sześcioma różnymi parami punktów były tylko dwie różne odległości? Jedno rozmieszczenie bardzo łatwo znaleźć – cztery punkty są wierzchołkami kwadratu.
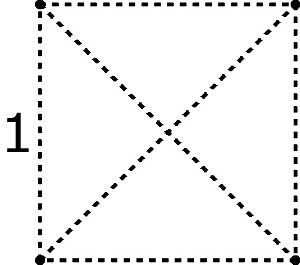
Odległości nie są już zapałkami, a więc – jak wynika z rysunku – mogą się przecinać. Dłuższa odległość miedzy parami punktów, czyli przekątna kwadratu, równa jest sqrt2.
Proszę znaleźć wszystkie pozostałe układy czterech punktów i podać w przypadku każdego z nich większą odległość między punktami przy założeniu, że mniejsza równa jest 1.

Komentarze
Znalazlem jeszcze dwa ulozenia o „dlugosci” odpowiednio: sqrt(3) i 3. No i chyba wiecej nie ma… A zadanie o zapalkach jest moim zdaniem dosc proste 🙂 . Podobne w zamyśle jest zadanie: jak łamaną o 4 odcinkach pokryc 9 punktow (ulozonych w kratę 3 x 3)?
niezły blog ;p